1) To construct a tangent to a circle (0) through point Q you need to construct the midpoint of OQ. Next you need to construct a circle with the center as the midpoint you constructed and Q as a point on the circle. The line that passes through Q and the intersection of the two circles is the tangent to circle O through P.
The mathematical fact we observed was that a tangent of a circle makes a right angle with the radius at that point.
2) To construct an external tangent to two circles you must construct parallel lines through the centers of the two circles. Next, we found the points of intersection and constructed a line passing through the upper two points and the lower two points. This gave us our center of symmetry point. Then we constructed a tangent to one of the circles through the center of symmetry.
3) Monge's Theorem: The center of symmetries of any three circles are collinear.
4) Yes, there does exist a dilation but it is not unique. The dilation would have a center C which would be any point on the line AA'.
Yes, there does exist a dilation and yes it is unique. The center of dilation is the point intersection of AA' and BB'. Since a pair of lines only intersects in one point, this center is unique.
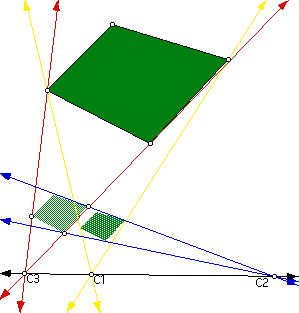
5) The first step in showing that the three centers of dilation are collinear is to show that the composition of two dilations is a third dilation. This can easily be shown using the transitive property. If figure A under dilation produces figure B and figure B under dilation produces figure C, then figure A must produce figure C under dilation.
The second step is to show that the center of composition (C3) lies on the line through the other two centers (C1 and C2). In problem number 4 we picked four points on the plane and dilated them about C1 and C2 which resulted in a third dilation with center C3. We could have taken any point on the plane and dilated it to see its image, we just happen to pick four points and study their particular images. Thus we can restrict our study only one point on the plane and its image.
Take a point P collinear with C1 and C2. Dilate P by any ratio about the center C1 and P1 will be a the line throuh C1 and C2. Now dilate P1 by any ratio about C2, P2 will also be on the line through C1 and C2. To get from P to P2 we took a compositon a dilations, thus there is a new dilation with center C3 that takes P to P2. This new center must be on the line through P and P2 and since P and P2 and collinear with C1 and C2, C3 must also be collinear with C1 and C2.
6) We learned that Monge’s theorem can be applied to three dimensions. In two dimensions we already seen that the external tangents of three non-uniform spheres lie on a line. Likewise, the web site showed that if we add one more sphere to the problem the external tangents will all lie on a plane.
7) Theorem: The intersection points of the opposite sides of a hexagon inscribed in circle will be collinear.