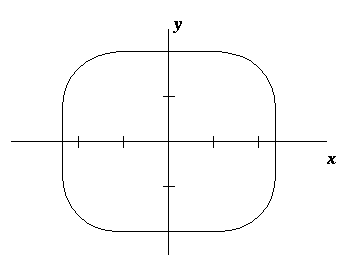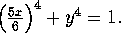Areas of Some Models for a Domed Stadium

In this section of the lab, we will estimate the area bounded by models for a domed stadium. Naturally, our answers are only as good as our mathematical models.

We will make the following assumption: the length of our stadium is 1.2 times the width. We will normalize the problem so that the length of the stadium sits along the x-axis from -1.2 < x < 1.2 and the width of the stadium is oriented with the y-axis from -1< y < 1. See Figure 2.

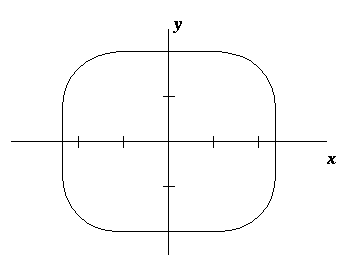
Figure 2: Looking down at a model of the Metrodome.

As we did last week, we will use T. Murdoch's calcplot package to help us plot some graphs. In your Maple window, issue the command

     read `/u/calcIII/calcplot.m`;

Activity #1

(You do not need to include this activity in your lab writeup.) The very crudest approximation for the stadium is if we approximate the shape of the stadium by a rectangle. Since in reality the metrodome has curved sides, this will overestimate the area enclosed by the stadium.

Set up an iterated integral for the area of the rectangle satisfying -1.2< x < 1.2 and -1< y < 1.
Although the domain is trivial to sketch by hand, use the dydxplot command to plot the region of integration:
dydxplot(y=-1..1, x=-6/5..6/5);
Although the integral is trivial to solve by hand, use Maple to compute the integral for the area:
int( int(1, y=-1..1), x=-6/5..6/5);
Note the similarity in the syntax of these two commands.
Why is the integrand of the previous integral equal to 1?

Question #1

A different model for the stadium is to assume the the walls of the Metrodome are approximately given by the ellipse with axes of length 1.2 and 1.

Set up an iterated integral for the area of the ellipse.
Use the dydxplot command to plot the region of integration:
dydxplot(y=-sqrt(1-(5*x/6)^2)..sqrt(1-(5*x/6)^2), x=-6/5..6/5);
Sketch this region in your lab report.
Compute the integral to find the area of the ellipse.

Question #2

A more sophisticated models postulates that the walls of the stadium satisfy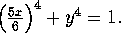

As before,

Set up an iterated integral for the area enclosed by this curve.
Use the dydxplot command to plot the region of integration. Sketch this region in your lab report.
Compute the integral to find the area. (Hint: Maple will be unable to symbolically solve the integral. Use the evalf command to evaluate the integral numerically.)

Question #3

As part of your lab report, comment on the models above and how well you think they correspond to reality. For example you may want to consider:

What is the scale factor in this problem (eg, 1 unit equals how many feet)?
Can you think of a better model for the Metrodome walls?
What geometric features are important to model the area?

Here are some Metrodome facts to help you make informed decisions.

Next: Volumes of our Models
Previous: Computing Areas and Volumes

Frederick J. Wicklin<fjw@geom.umn.edu>

Document Created: Sun Jan 8 1995
Last modified: Wed Jan 18 12:49:22 1995