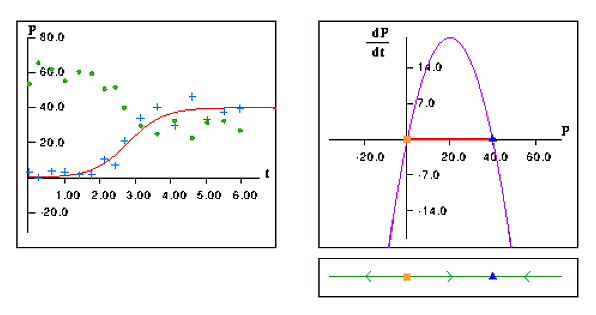
The students are then introduced to logistic growth and are asked to model, speculate, and defend whether the post-glacial influx of white pine ( Pinus strobus) into northeastern Minnesota is accurately modeled by a logistic growth (see Figure 2). The numerical data for this problem was generated by counting pollen grains in deep-lake laminated sedimentary cores [Craig].
After learning about equilibria, the students are asked to model the deer population in Minnesota and to numerically investigate how the issuing of hunting licenses affect the population of that model. Based on the data they generate, students evaluate whether hunting is an effective method of controlling the size of the deer population.
The interactive portion of this lab is a ``Population Simulator'' that permits the student to choose parameters that specify a particular differential equation from within a three-parameter family of differential equations. The student may then numerically integrate a trajectory starting from an initial condition (chosen by clicking with a mouse). The simulator displays time series of multiple trajectories, superimposes experimental data, solves for equilibria, and displays the phase space for the current population model.