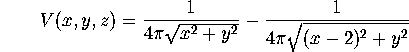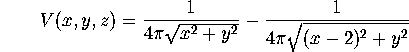Electromagnetic Potentials
Consider two electric charges, one positively charged and the other negatively
charged. Let's put one "unit" of positive charge at the origin and
one unit of negative charge on the x-axis
at the point x=2. The electric potential created by these
two charges is very similar to the gravitational potential that we've studied
in other labs: the electric field is given by the opposite of the
gradient of the potential. The intensity of an electric field may be
pictured by looking at the
intensity of the so-called field lines as shown in Figure 1.

Figure 1: The intensity of an electric field is proportional to
the number of field lines per unit area (perpendicular to the
lines). Thus the field is strong when the field lines are close
together and weak when the field lines are far apart.
Let's start out by investigating the geometry of the electric field.
To begin, let's pretend that the charges live in a 2D world. Then
the electric potential that they generate is
proportional to
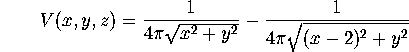
Let's begin our study by preparing Maple to
access it's linear algebra and special plotting functions:
with(linalg): with(plots):
We can then define V to be the 2D electric potential :
V:= 1/(4*Pi*sqrt(x^2+y^2)) - 1/(4*Pi*sqrt((x-2)^2+y^2));
Question #1
Use the plot3d command to visualize the
electric potential V for x=-0.5..2.5
and y=-1..1. Hint: You may want to
use the option view=-1..1 in order to
better see the essential features of the graph.
To visualize the vector field known as the electric field, issue the command
gradplot( -V, x=-0.5..2.5, y=-1..1, grid=[10,10] );
- Explain how the vector field you see is related to the
graph of the potential function V.
- Describe how the field lines in Figure 1 related the to electric field.
- Physically, the electric field at the point (x,y)
represents the force that a
small positively-charged "test particle" will feel if placed at (x,y).
Describe the force (magnitude and direction) on a
test particle if it is located in the regions
- Use the fact that the electric field is the negative gradient of the
electric potential (that is, E=-grad(V))
to descibe the intensity (or magnitude)
of the electric field at various locations
in the xy-plane.
Next: 3D Flux through a Plane
Previous: Introduction
Frederick J. Wicklin<fjw@geom.umn.edu>
Document Created: Fri Mar 31 1995
Last modified: Mon Apr 3 16:14:33 1995