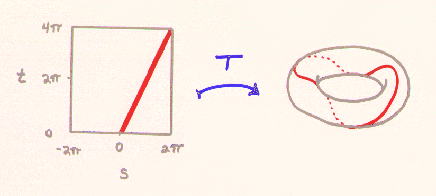Torus Knots
For this lab, you will want to load some standard Maple packages:
with(plots): with(linalg):
(Maple will give you a Warning message; this is normal.)
Recall that a torus may be parametrized by rotating a circle of radius r
about another circle of radius R. For concreteness,
let r=1 and R=2. Then a parametrization
of the torus may be written:
T(s,t) = ( (2+cos(t))cos(s), (2+cos(t))sin(s), sin(t) )
In Maple, such a function would be written as
T:=(s,t)-> [(2+cos(t))*cos(s),(2+cos(t))*sin(s),sin(t)];
A torus knot is a closed curve that winds around the torus.
You can generate torus knots by specifying an integral relationship between
the parameters s and t. For example, if
we restrict T to the curve t=2s, then we get a
parametrized curve
T(s,2s) = ( (2+cos(2s))cos(s), (2+cos(2s))sin(s), sin(2s) )
This curve wraps around the torus once in the "long" direction while
it wraps around the torus two times in the "short" direction, as indicted in
Figure 1.
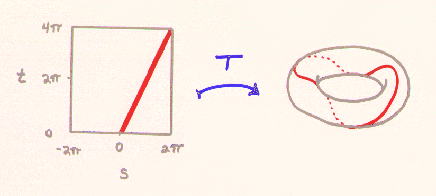
Figure 1. The mapping that takes the curve t=2s to the torus knot
of type (1,2).
In general, for nonzero integers m,n, a
torus knot of type (m,n)
is the image of the line ns=mt + const. (The constant moves
the knot around, but doesn't change the way that it winds.)
This image will wind around
the torus m times in one direction and n times
in the other direction. If either m=0 or n=0, then the
definition changes slightly: a torus knot of type (1,0) is the
image of the line t=constant whereas a knot of type (0,1)
is the image of a line s=constant.
Question #1
For each of the torus knots below, imitate Figure 1 to sketch a line in
parameter space and the image of that line on the torus. When a point is given,
indicate that point and its image on the sketch.
Hint: Look up the Maple spacecurve command to help you plot
the image of the curve on the torus.
- Knot of type (1,0) and including the point (s,t)=(0,Pi/2)
- Knot of type (1,0) and including the point (s,t)=(0,3 Pi/2)
- Knot of type (1,1) and including the point (s,t)=(0,0)
- Knot of type (1,1) and including the point (s,t)=(0,Pi)
- Knot of type (2,1)
Next: Building a Surface from Torus Knots
Previous: Introduction
Frederick J. Wicklin<fjw@geom.umn.edu>
Document Created: Thu Feb 23 1995
Last modified: Wed Mar 1 15:07:46 1995