A Brief History of the Pythagorean
Theorem
Just Who Was This Pythagoras, Anyway?
Pythagoras (569-500 B.C.E.) was born on the island of Samos in
Greece, and did much traveling through Egypt, learning, among
other things, mathematics. Not much more is known of his early
years. Pythagoras gained his famous status by founding a group,
the Brotherhood of Pythagoreans, which was devoted to the study
of mathematics. The group was almost cult-like in that it had
symbols, rituals and prayers. In addition, Pythagoras believed
that "Number rules the universe,"and the Pythagoreans gave
numerical values to many objects and ideas. These numerical
values, in turn, were endowed with mystical and spiritual
qualities.
Legend has it that upon completion of his famous theorem,
Pythagoras sacrificed 100 oxen.
Although he is credited with the discovery of the famous
theorem, it is not possible to tell if Pythagoras is the actual
author. The Pythagoreans wrote many geometric proofs, but it is
difficult to ascertain who proved what, as the group wanted to
keep their findings secret. Unfortunately, this vow of secrecy
prevented an important mathematical idea from being made public.
The Pythagoreans had discovered irrational numbers! If we take
an isosceles right triangle with legs of measure 1, the
hypotenuse will measure sqrt 2. But this number cannot be
expressed as a length that can be measured with a ruler divided
into fractional parts, and that deeply disturbed the
Pythagoreans, who believed that "All is number." They called
these numbers "alogon," which means "unutterable." So shocked
were the Pythagoreans by these numbers, they put to death a
member who dared to mention their existence to the public. It
would be 200 years later that the Greek mathematician Eudoxus
developed a way to deal with these unutterable numbers.
The sum of the squares of the sides of a right triangle is
equal to the square of the hypotenuse.
This relationship has been known since the days of the ancient
Babylonians and Egyptians, although it may not have been stated
as explicitly as above.
A portion of a 4000 year old Babylonian tablet (c. 1900 B.C.E.),
now known as Plimpton 322, (in the
collection of Columbia University, New York), lists columns of
numbers showing what we now call Pythagorean Triples--sets of
numbers that satisfy the equation
a^2 + b^2 = c^2
Euclid, in his book The Elements, presents a proof of the
Pythagorean Theorem.
*Hands On Activity*
It is known that the Egyptians used a knotted rope as an aid to
constructing right angles in their buildings. The rope had 12
evenly spaced knots, which could be formed into a 3-4-5 right
triangle, thus giving an angle of exactly 90 degrees. Can you make a rope like this? Now use your knotted rope to check some right angles in your room at school or at home.
A Babylonian Tile Proof
There is further evidence that the Pythagorean relationship was
known before the first written proof of it. The pattern of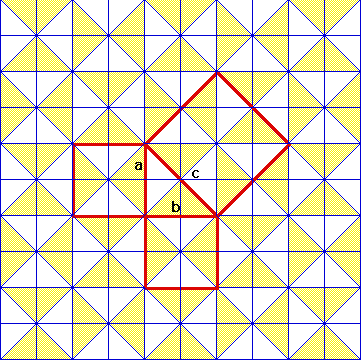 
tiles
shown here is typical of those seen
in the Orient.
Can you see the proof of the Pythagorean Theorem in the tile
pattern?
Click here for an explanation of the proof.
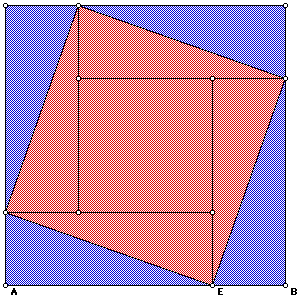
Challenge Yourself!
The Chinese used the Pythagorean Theorem as far back as 1000
B.C.E. Can you figure out the method of proof used in the figure below?
A Sketchpad Excursion
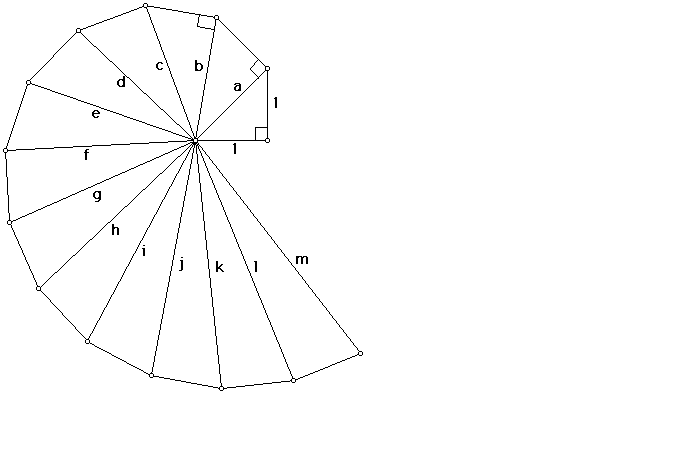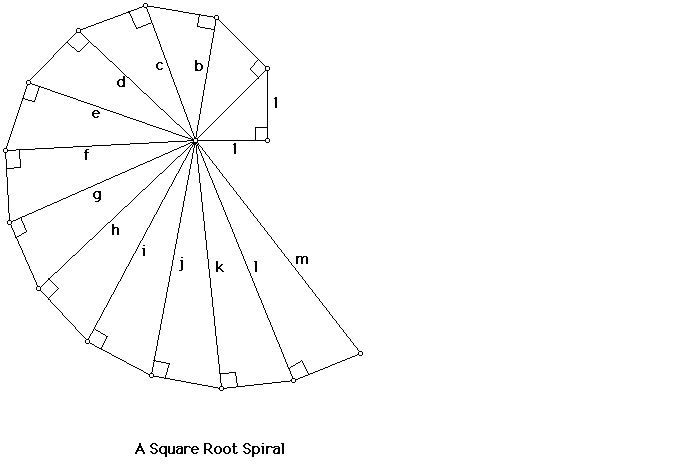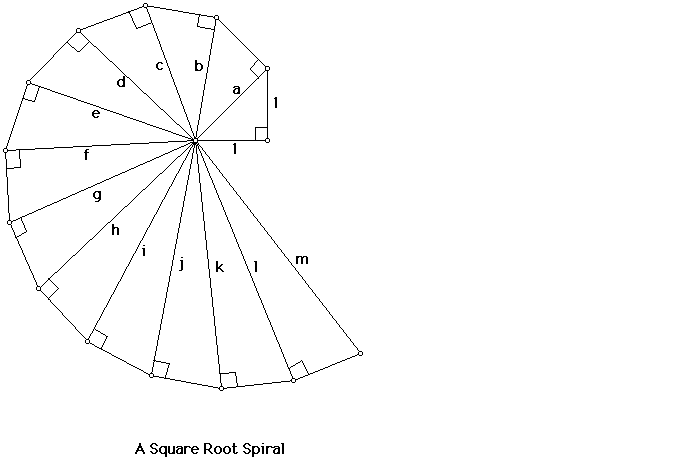
The Pythagoreans discovered, but refused to recognize the
existence of, irrational numbers. By starting with an isosceles
right triangle with legs of length 1, we can build adjoining
right triangles whose hypotenuses are of length sqrt 2, sqrt 3,
sqrt 4, sqrt 5, and so on. This construction is sometimes
referred to as the Square Root Spiral.
Click here
or on the picture to get an interactive sketchpad sketch.
Questions to explore:
- Can you construct a segment whose length is sqrt 15?
- Can you develop a more direct
method of constructing a segment whose length is sqrt 12?
???Did you know???
- There are over 250 Proofs of the Pythagorean Theorem.
- President Garfield did an original proof of the Pythagorean Theorem.
- Many years ago, an original proof of the Pythagorean Theorem was a requirement for a Master's Degree in Mathematics.
Beyond the Pythagorean Theorem
In the 17th century, Pierre de Fermat(1601-1665) investigated the following problem: For which values of n are there integral solutions to the equation
x^n + y^n = z^n
We know that the Pythagorean theorem is a case of this equation when n = 2, and that integral solutions exist. Fermat conjectured that there were no solutions when n was greater than 2. He did not leave a proof, though. Instead, in the margin of a textbook, he wrote that he knew that this relationship was not possible, but he did not have enough room on the page to write it down.
His conjecture became known as Fermat's Last Theorem. This may appear to be a simple problem on the surface, but it wasn't until 1993 that Andrew Wiles of Princeton University finally proved the theorem.
References
Kramer, Edna E., The Main Stream of Mathematics From the Earliest Beginnings to the
Age of Relativity,
New Jersey, The Scholar's Bookshelf, 1988.
Loomis, Elisha Scott, The Pythagorean Proposition, Washington, D.C.,
The National Council of Teachers of Mathematics, Inc., 1968.
Pearson, Helen and Lightner, James, Geometry, Annotated Revised Edition,
Lexington, Massachusetts, Ginn and Company, 1984.
Return to Main Menu
