The Pregol'a River flows through
the city of Kaliningrad, in Russia ( Check out Kalinigrad's
web page). There are two islands in the river, and seven bridges
connect the island to each other and to the shores. In the 1700's,
this city was part of East Prussia and was known as Konigsberg. It
was common on Sunday for people to take walks over the bridges. These
walks and bridges led to a problem. Over time this problem reached
the famous mathematician
Leonhard Euler (pronounced "Oiler") (You can find more information about
Euler here).
Euler described the problem himself in the following letter:
The problem, which I understand is quite well known, is stated as follows: In the town of Konisberg in Prussia there is an island called Kneiphof, with two branches of the river Pregel flowing around it. There are 7 bridges - a, b, c, d, e, f, and g - crossing the two branches. The question is whether a person can plan a walk in such a way that he will cross each of these bridges once but not more than once. I was told that while some denied the possibility of doing this and others were in doubt, no one maintained tht it was actually possible. On the basis of the above I formulated the following verygeneral problem.....
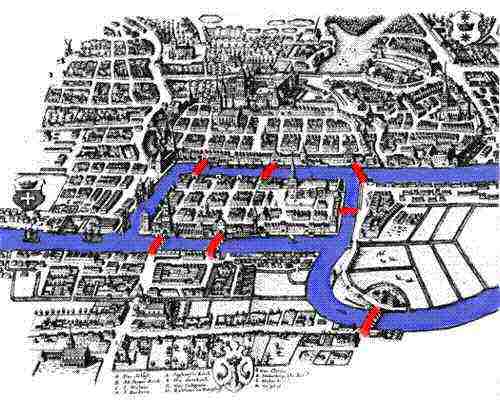
Euler came up with a theory that solved this problem. This lead to the creation of a new branch of mathematics called graph theory.
To understan Euler's solution to this problem we will reconstruct his steps.
|
|
|
|
|
|
|
|