 FIBONACCI IN NATURE
FIBONACCI IN NATURE
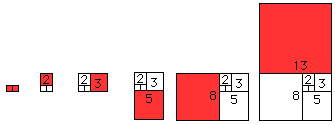
We will construct a set of rectangles using the Fibonacci numbers 1, 1, 2, 3, 5, 8, 13, 21, and 34 which will lead us to a design found in nature. You will need a ruler, protractor, and compass.
Start by drawing two, unit squares (0.5 cm is suggested) side by side. Next construct a 2-unit by 2-unit square on top of the two, unit squares. Next draw a square along the edge which borders both a unit square and the size 2 square (that is, a 3-unit square). The next square will border the 2-unit and the 3-unit squares, and each successive square will have an edge which is the sum of the two squares immediately preceding it. Continue until you have drawn a final square bordering the 13-unit and 21 unit squares.
Your construction will look like this:

Now, with your compass, starting in the unit squares, construct in each square
an arc of a circle with a radius the size of the edge of each respective
square (Your arcs will be quarter circles.).
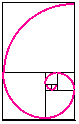
This spiral construction closely approximates the spiral of a snail, nautilus,
and other sea shells.

We will next consider the use by architects and artists throughout history of
the "Golden Ratio" and other
geometric shapes based upon these ratios.