The Golden Ratio

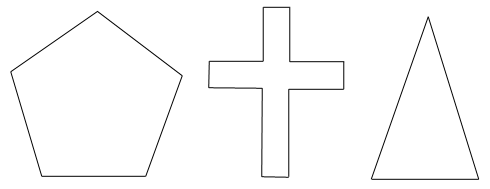
You can do the following explorations by using a protractor to draw on paper, or by using Geometer's Sketchpad.

REGULAR PENTAGONS

Draw a regular pentagon (to get you started recall that the interior angles have measure 108 degrees) and also draw in one diagonal of the pentagon. Measure the length of one side of the pentagon and measure the length of the diagonal. What is the ratio of the side to the diagonal?

GRAVEYARD CROSSES

A German psychologist by the name of Gustav Fechner studied the crosses in graveyards and discovered an interesting fact about their dimensions. Measure the upper and lower portions of the main stem of the cross which is cut by the crossbar. What is the ratio of the lengths of these two portions?

ISOSCELES TRIANGLE

Draw an isosceles triangle with base angles equal to 72 degrees. Measure the length of the shorter side and the two legs, which of course have the same length since this is an isosceles triangle. What is the ratio of the lengths?

Now rotate the shorter side through the base angle until it touches one of the legs. From the endpoint draw a segment down to the opposite base vertex. The original isosceles triangle is now split into two triangles. Calculate the area of the two smaller triangles. What is the ratio of the areas?