An Investigation of
Perpendicular Bisectors in a Triangle
Background
In this section of the exploration you will be asked to discover the way the perpendicular bisectors of a triangle relate to each other. As you work through the material, you may be asked to write down the answers to the questions in the investigation or to save the information and your sketch on a disk. Ask your teacher for specific directions.
Exploring the Perpendicular Bisectors of a Triangle
Click on the image below to activate the Geometer's Sketchpad Triangle Sketch. You are going to use this sketch to construct the perpendicular bisectors of a triangle. The instructions for the construction are below the picture. Following the construction, you will use your sketch to investigate relationships involving the perpendicular bisectors.
Construct
- Construct the perpendicular bisector to side AC.
- Directions for construction of a perpendicular bisector.
- Script for constructing a perpendicular bisector.
- Construct a second perpendicular bisector in the triangle to side AB.
- Make a point at the intersection of these two perpendicular bisectors.
- Construct the third perpendicular bisector to side BC. Take a break here to work on questions 1 to 3 in the investigation section.
- Construct a circle centered at the concurrency point. Make the radius of the circle coincide with one of the triangle vertices. Answer question 4.
- Construct three segments, one from each vertex to the point of concurrency. Measure each segment and record your results as part of question 5.
Investigate
- When you constructed the third perpendicular bisector, did it pass through the same point as the other two perpendicular bisectors?
- Use the selection tool (the arrow) to move the vertices of the original triangle. Do the perpendicular bisectors intersect when the shape of the triangle is changed?
- Write a conjecture about the way the perpendicular bisectors intersect in a triangle. (Check your answer.)
- When you drew the circle, what relationship was formed with the other two vertices? Did the position of the circle change, with respect to the vertices, when you changed the shape of your triangle? (Check your answer.)
- Record your measurements here. How are the lengths of the segments related? (Check your answer.)
We call the intersection of the perpendicular bisectors of a triangle the circumcenter of the triangle. The circle that you drew is called the circumcircle.
An Exploration of the Circumcircle and the Path of its Simson Line
A Simson Line is a special line drawn to the sides of a triangle. It is not too difficult to construct but it has an amazing property. Click on the sketch of the triangle and it's circumcircle and follow the instructions to construct the Simson Line. In the process, you will learn a little about animating sketches.
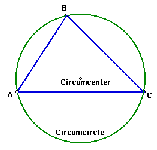
- Select the circumcircle and construct a point on it. The point should move freely.
- Draw and select line AB the point on the circle you just constructed. Construct a perpendicular line and the intersection point of the two lines. Hide the two lines. The intersection point should remain visible.
- Repeat the process above on side AC.
- Repeat the process again on side BC.
- Connect two of the three intersection points with a line. This line is a Simson Line. The third intersection point should also lie on your line.
- Select the Simson Line and use the color option of the Display Menu to change the color.
- Select the line again and pull down the Display Menu to Trace Line. This will make the path of the line visible when you animate.
- Now you want to look at what happens to the Simson Line when the point you constructed in Step 1 moves around the circumcircle. To do this select the point and the circumcircle. Pull down the Display Menu to animate.
- When you let go of the mouse at Animate you will get a Path Match box. Just click on Animate and you will see the path traced by the Simson Line.
If you had difficulty with the sketch above, you can click here to see the path of the line. This curve is a deltoid.
Before you leave this investigation....
Did you follow your teacher's directions about saving your work and turning it in?
Next: Go Back