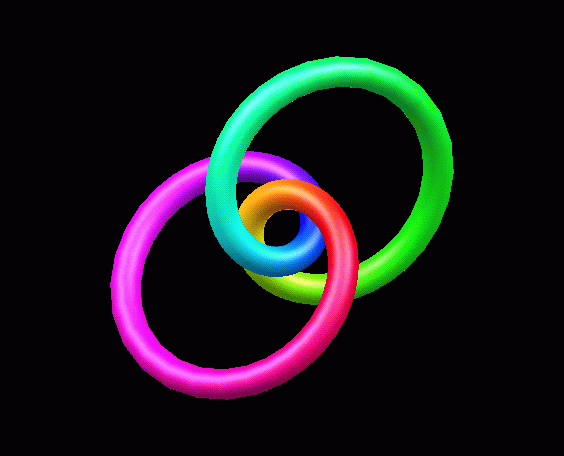
What about a curve on the three-sphere? One approach is to project the curve stereographically into three-space and to take the self-linking number of the resulting space curve. This does not work for the simple reason that the self-linking number can be different for projections from different points. This raises the question about the actual self-linking number on the three-sphere and its relationship with the self-linking numbers of the projections into three-space.
To see a curve on the three-sphere rotating in red and white, activate the movie
To see a curve on the three-sphere rotating with strange colors, activate the movie
To see a curve on the three-sphere rotating with nice colors but low resolution, activate the movie
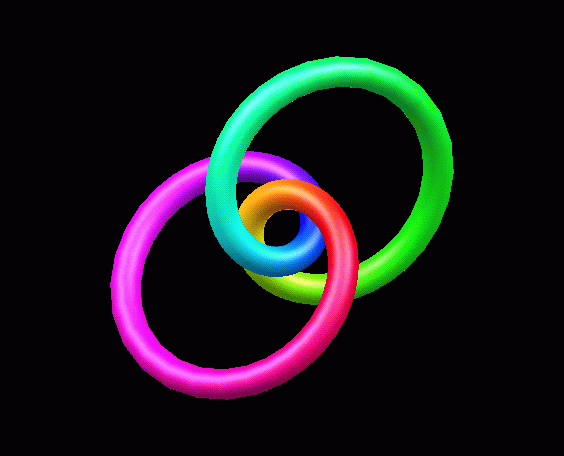
3/6/95 banchoff@geom.umn.edu --
The Geometry Center