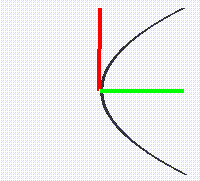

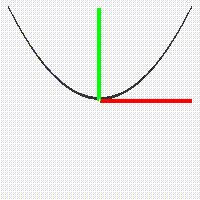
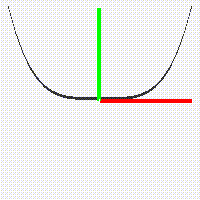
Similarly the graph of the function u = x^2 fits inside a square in the plane, as do the graphs of all the other power functions u = x^n for positive integers n.
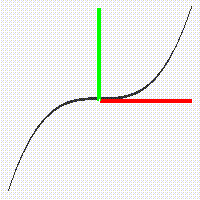
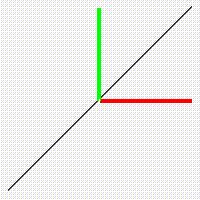
It is interesting and important to observe that a good graph of a monotonic function like u = x or u = x^3 automatically provides a good graph of its inverse function. In the case of the identity function the inverse is also the identity x = u, and in the case of the cubing function, the inverse is the cube root u = x^1/3.
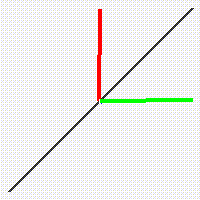
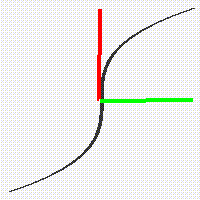
We obtain the graph of these inverse functions by the simple device of rotating the graph about the diagonal of the square.
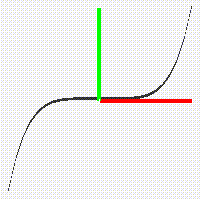
If we apply the same transformation to the graph of the squaring function we do not obtain a function graph since above the points of the positive u-axis we have two values for the square root. However the rotated graph of the squaring function does give the graph of the square root relation.