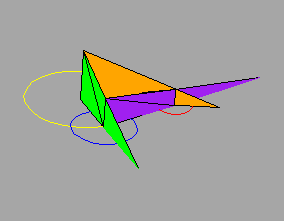
(To see a representation of this theorem use the interactive sketchpad.)
A version of Desargues' Theorem says that if two triangles have their corresponding vertices on three parallel lines, then the intersections of the lines containing the corresponding sides will be collinear.
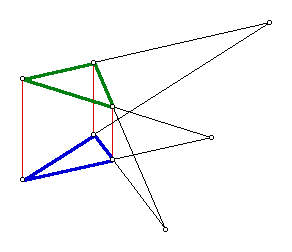
(To see a representation of this theorem use the interactive sketchpad.)
In a strong sense, these two theorems are the same theorem in two different guises.
The key observation is that the point of intersection of the external tangents of two non-nested circles is the same as the intersection of the line joining their centers with any line joining corresponding points on the circles, in particular the "north poles", the highest points on the circles in the vertical direction.
Thus the configuration of three circles with external tangents leads to the same three points of intersection as the configuration of two triangles, one with vertices at the north poles of the circles and the other at south poles. Thus the two theorems imply each other.
One corollary that follows from this observation is that it is not necessary to require that the original circles be disjoint, although at this stage we still do not want any circle to be situated inside another. In particular, if two circles are internally tangent, the point of tangency is the limit of intersections of external tangents as two intersecting circles move to become tangent. Thus the theorem will work for three circles even when two of them are internally tangent, or even when two pairs have internal tangency.
We may also observe that Desargues' theorem remains correct if the south pole and the north pole of one of the circles reverse directions, in which case we deal not with the external tangents but the internal tangents between the corresponding circles. We may think of the circles as being oriented, so the tangencies that we take are the ones that respect the orientation, namely the external tangencies when the two circles have the same orientation and the internal ones when the orientations are opposite. Thus if we have three circles, none contained in the interior of the other, we may form the intersection points of "oriented tangents", again obtaining a collinear triple, either consisting of the external tangency intersections or one external tangency intersection and two internal ones.
Once we realize that the points of intersections of external tangencies are really the centers of dilatation taking one circle (or oriented circle) into another, there is no reason to require that no circle intersects or lies inside another. Given any two circles of unequal radii, there is a unique center from which the one may be obtained from the other by dilatation. The three dilatations centers are then collinear. Note that in certain cases, two or more of the dilatations centers can coincide, for example when the corresponding circles are concentric. But it was always possible for three circles to share the same pair of external tangencies, so in this case the three intersection points would automatically be coincident, therefore a fortiori collinear.
The theorem of Monge generalizes to quadruples of spheres, in the sense that the lines of intersection of externally tangent planes will all lie in the same plane. If we take any pair of non-nested spheres of different radii, then there is a unique center of dilatation from which it is possible to scale on sphere into the other. There are six pairs of spheres so we obtain six points in this way. Any three of the spheres will determine three such points lying on a line. If we exchange one of these spheres for the fourth sphere, we get another line, through the common center of dilatation of the common pair of spheres. Thus five of the six points already lie on a plane, and since the sixth point lies on a line joining two of the others already in the plane, one on each of the two lines already constructed, it follows that all six points, and the lines they determine, lie in the same plane.
If the program Fnord runs on your machine, then you can investigate these phenomena interactively, by accessing Fnord.
For more discussion of these theorems, see for example, Geometry and the Imagination by Hilbert and Cohn-Vossen.