If you have the program Fnord running on your machine, then you can investigate the following phenomena interactively, by activating Fnord.
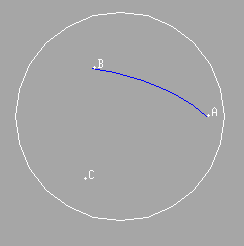
We start by choosing two distinct points A and B on a hemisphere. The two points and the origin of the sphere determine a plane, and the intersection of the plane and the sphere gives the great circle through the two points. The part of the great circle between the two points on the hemisphere is called the segment BC determined by the points.
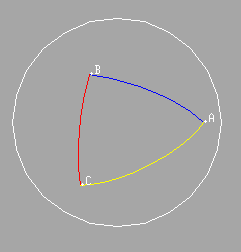
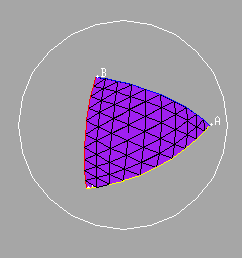
Given three distinct points A, B, and C on a hemisphere, we can show the three segments AB, BC, and CA to give the edges of the triangle ABC. We can then fill in the region in the hemisphere bounded by the edges of the triangle, to obtain the triangular region determined by A, B, and C.
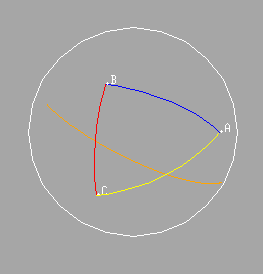
Given any two points A and C on a hemisphere we can construct the midpoint of the segment AC. Given three distinct points A, B, and C on the hemisphere, we can construct the great circle through the midpoints of segments AC and BC.
Through the point A, we may construct the great circle perpendicular to any given great circle G. The intersection of these two great circles lying in the hemisphere is called the foot of the perpendicular from A to the great circle G.
Using this construction, we may indicate the segment from A to the foot of the perpendicular from A to the great circle through the midpoints of AC and BC.
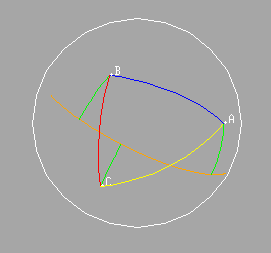
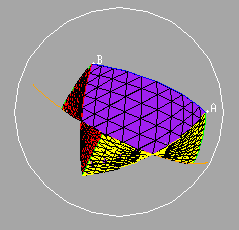
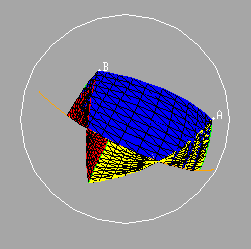
Similarly we may indicate the segments from B and C to the feet of the perpendiculars from these points to the great circle through the midpoints of AC and BC. These two segments, together with the segment BC itself and the segment joining the feet of the two perpendiculars will give the edges of a quadrilateral on the sphere, the so-called Saccheri quadrilateral of the triangle on the edge AB.
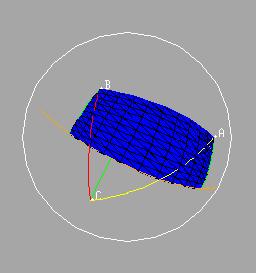
It is not difficult to show that the area of this quadrilateral is equal to the area of the original triangle. Observe that the yellow triangles are congruent since they are right triangles with equal hypotenuses and with equal (vertical) angles.
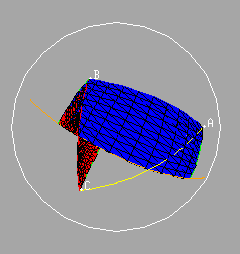
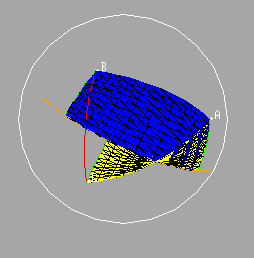
It follows that the area of the original (purple) triangle is equal to the area of the Saccheri quadrilateral erected on the side AB.