Peaucelleir's Linkage
Problem 2
Problem 3
Problem 4
Problem 5
Problem 6
Problem 7
Problem 8
Problem 9
1. Peaucellier's linkage.
Back to top
Back to top
3.The Definintion of Inversion (AF)(AF')=r^2
- The inverse of a point inside a circle is a point outside
of a circle.
- If (AF) smaller than r, and (AF)(AF')=r^2, then
(AF') must be bigger than r, so F' will lie
outside of the circle.
- The inverse of a point outside the circle is a point
inside the circle.
- A point on the circle is it's own inverse.
- If (AF)=r, and (AF)(AF')=r^2, then (AF')=r
- The inverse of the center of the circle is infinity.
- As (AF) approaches 0, (AF') approaches infinity,
so that (AF)(AF') can be defined.
Back to top
4. Table 2C
| Shape inverted |
Inverse of shape |
| Circle through A |
Line |
|
| Circle not through A |
Circle |
|
| Line through A |
Line through A |
|
| Line not through A |
A Circle |
|
Back to top
5. Constructing the inverse of a circle
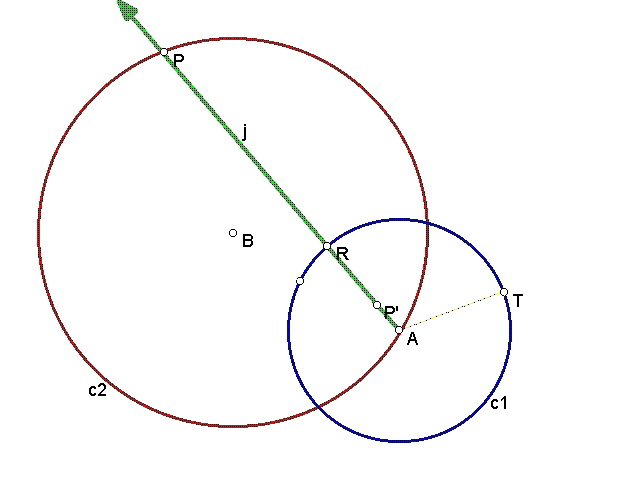
- Construct Circle 1 (c1) with A as it's center.
- Construct Circle 2 (c2) with center B, and Radius AB.
- Construct a Point P on c2.
- Construct Ray AP.
- Label Point R at the intersection of RayAP and c1
- Construct Segment AP
- Choose a point on c1, label it T. Make segment AT.
- Select AP, and then AT, and mark the ratio.
- Choose A as your Center of Dilation, and dilate P by the
marked ratio above.
- Label this point P'.
- Trace P'
- Move P around c2 to get the inverse of c2.
Back to top
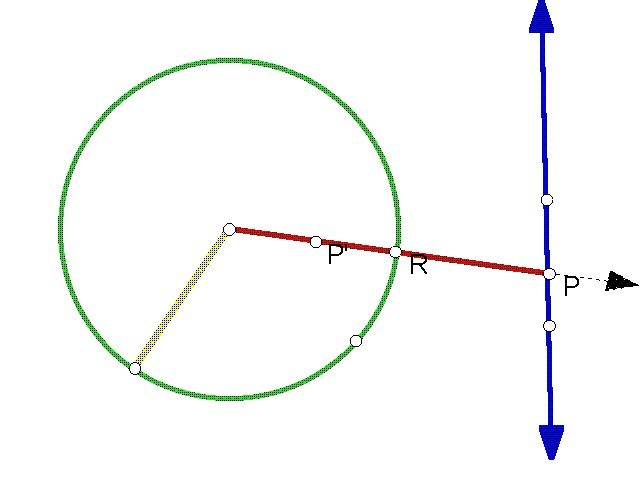
6. The inverse of a line not through the center of the circle of inversion.
Back to top
Script
- Construct c1 with A as center.
- Construct line j, not intersecting c1.
- Choose P on j, to be inverted.
- Construct Ray AP
- Mark R as the intersection of AP and c1.
- Construct Segment AP
- Make a radius segment from A to a point on c1.
- Select radius segment, hold down Shift key and select Segment AP. Mark ratio.
- Select A to be your Center for Dilation.
- Dilate R by marked ratio.
- Name dilated point P', trace this point.
- Move P along the line to get the inverse of line j.
Back to top
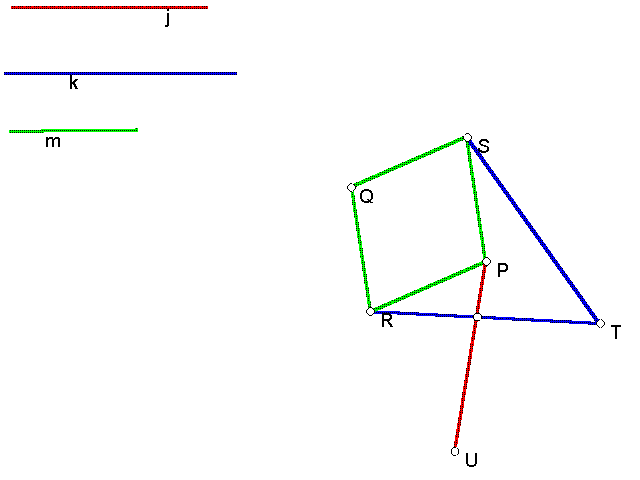
7. P and Q are related by inversion.
The definition of inversion through circle of radius r centered at A: The inverse F' of a point F is such that A,F, and F' are collinear, and (AF)(AF')=r^2.
Using the sketch above, a line can be drawn through T,P, and Q. (They are collinear.) Calculations show that (TP)(TQ)=(TU)^2. Thus, P is the inverse of Q, TU is the radius, and T is the center of the circle of inversion.
Back to top
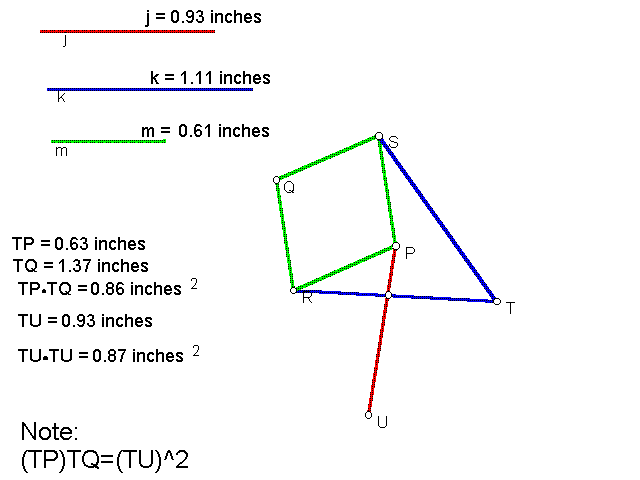
8. Peaucellier's Linkage with the circle of inversion.
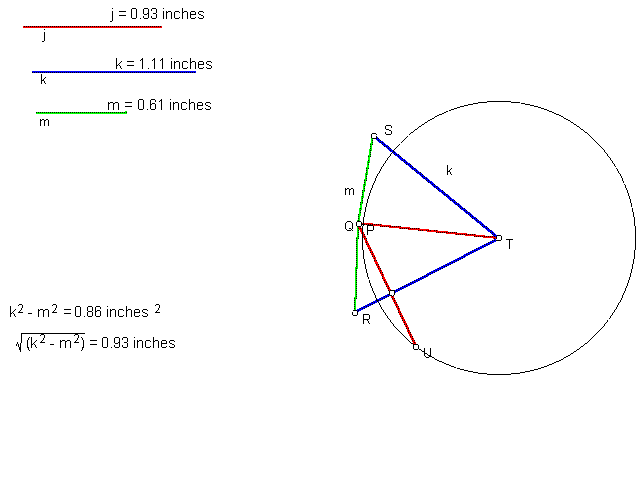The radius of the circle can be found when P lies on top of Q. We know that at that point, TP=TQ=the radius of the circle. When constructing this line,notice the right triangle with leg m and hyp k. Using the Pythagorean theorm, r^2=k^2-m^2, so r=The square root of (k^2-m^2)
Back to top
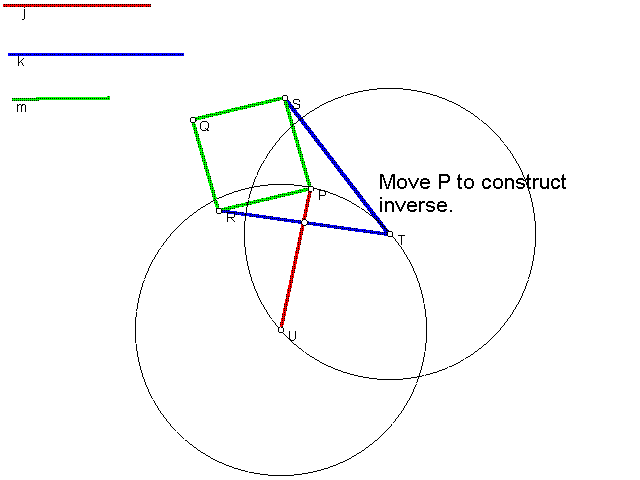
9. A sketch of the inverse of the circular path of P.
Back to top