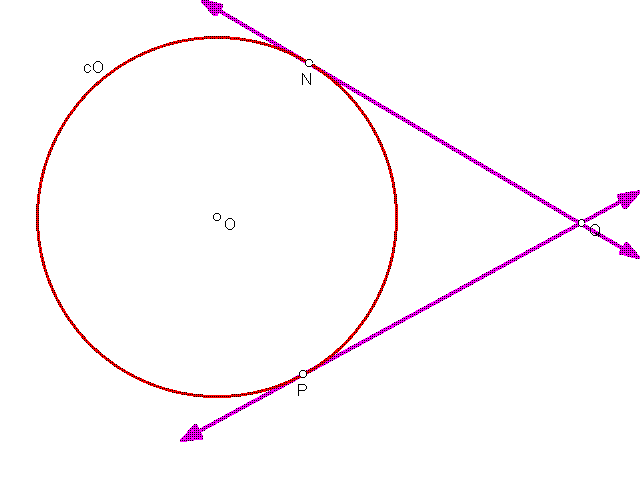
1. Make CircleO (with center O)
2. Make point Q not on CircleO.
3. Construct segment OQ.
4. Construct midpoint of OQ, call it M.
5. Construct CircleM with radius MQ.
6. Label the intersection points of CircleM with CircleO, N and P.
7. Draw NQ and PQ
8. Hide line OQ and Cicle M, if desired.
The CircleM constructed with the procedure above intersects CircleO at its tangent points. These tangent points are on a line OP(ON) that was constructed to be perpendicular to the line PQ (NQ). A mathematical fact to be observed is that the tangent lines are perpendicular to the radii (lines ON,OP) of the circle at the tangent points.
Script for Sketch of External Tangent
1. Make Circle01 and Circle02
2. Draw line l through the center of Circle01.
3. Construct a parallel line through the center of Circle02
4. Each line intersects its circle in two oppoisite points. Pick the upper point on each circle, and construct the line m through these points.
5. Construct a line through points 01 and 02 (the centers of the circles.). Label this line d.
6. Fine the intersection of line m and line d. Lable that point Q
7. Now we will procede to construct a tangent from point Q to circle02 (either circle would work)
8. Construct segment 02Q. Find the midpoint, and label it T.
9. Construct circleT with center at T and radius of TQ. Label the intersection of CircleT and Circle02, pointS. Construct line QS. This should be one external tangent. You may procede in a similar way to get the other external tangent or you may lable line d as your mirror line and simplly reflect line m. This will also produce an external tangent.
The lines containing the radii of Circles 01 and 02 were parallel to each other. When a tangent was constructed from point Q to Circle02, its radius was perpendicular to the tangent line. The radius of Circle02(parallel) would also be perpendicular to the tangent line. We found Q as a point that was contained in a line that passed through the radius of both circles, and passed through the common tangent line of both circles.
Interactive Sketch of Traced External Tangents
Script for Sketch of Traced External Tangent
Monge's Thoerem :
Given: Three Circles
Given: External tangents to each pair of circles.
Given: 3 Points of intersection of the tangents to each pair of circles.
Conclusion: The three points of intersection of the tangents lie in a line.
Script for Sketch of Illustration
Given two points A and A', there exists many dilations such that A' is the image of A'. To find one of the dilations, you must choose point C on lineAA' to be a center of dilation. Your scale for the dilation should be the marked ratio, mA'C/mAC
Given four points, A,A',B,andB', there does not exist a dilation sucn that A is the image of A', and B is the image of B'. However, if A and A' happen to be the external tangent points of a CircleA and a CircleB, and A' and B' happen to be the other corresponding pair of external tangent points, then a unique dilation does exist. If we were to find the point of symmetry described in part 2, this would be the unique center for dilation. Your marked ratio would again be mCA'/mCA.
The composition of two dilations is a third dilation. This third polygon (P'') is similar to the original polygon(P). Since P was dilated to P', P' is similar to P, by definition. Likewise, P'' is similar to P'. By the transitive property, P'' is similar to P. Therefore, P'' is a dilation of P. The three centers of dilation are coliniar. If we were to let Point S lie on the line containing C1 (center of dilation 1) and C2 (center of dilation 2), then S' would be on this line, and S'' would also be on this line. Therefore C3 must also lie on this line. Thus, for any point on polygon P that goes through a composition of dilations, C3 must lie on the line containing C1 and C2.
When two circles are related by a dilation, that dilation is unique. The center of this dilation must be the point where the external tangents meet. This point will be unique.
Monge's theorem is a based on a composition of dilations, and since the composition of two dilations is a third dilation, and these are colinear, the above argument also justifies Monge's theorem.
Desaurgues' Theorem, relating two triangles, is simply a compositon of dilations, dilating the parallel lines that are connecting the vertices of the two triangles. This relates directly to Monge's theorem, as a composition of dilations.
The document went on to generalize Monge's theorem to spheres, and the fact that any three spheres will determine thre centers of dilation lying on a line.
Theorem (my conjecture) If we extend opposite sides of a hexagon inscribed in a circle, those sides will meet in three distinct points, and those points will lie on a line.