The Shape of Our Universe

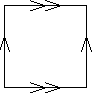If the shape of the flatlander's universe is a torus, then everything in their universe can be represented in a gluing diagram like the one at the right.

There are no boundaries in this space; the flatlander can travel forever in any direction. But that does not mean that there is an infinite amount of space and matter in their universe. Travelling in a straight line forever, the flatlander would pass the same stars again and again. Even though their space is boundless, it is finite (not infinite).

1. Which of the spaces below are boundless (i.e. a flatlander could travel forever in any direction)? __________________
2. Which have boundaries in all directions? __________________
3. Which have boundaries in some directions but not others? __________________
4. Which of the spaces are finite? ____________________
   a. b. c. d. e.

5. Which of the following are finite and which are infinite?
   1. a line? _______________
   2. a line segment? _______________
   3. a ray? _______________
   4. a circle? _______________

6. Is it possible for a space to be
   1. infinite and bounded in all directions? ____________
   2. infinite and boundless in all directions? ____________
   3. finite and bounded in all directions? ____________
   4. finite and boundless in all directions? ____________

What does this all mean about the three-dimensional universe we live in? It's possible that our universe is both finite and boundless. The following is from The Shape of Space video:

What seems to be a star in a distant galaxy could be our own sun. The light we receive from it could be light which left the sun billions of years ago, travelled around the universe, and is just now completing its trip. If we can someday find a pattern in the arrangement of the galaxies, then we will know the true shape of space.