Up: The Shape of Space Curriculum Materials: Symmetry and Tiling

Symmetry and 3-Dimensional Space

The Shape of Space Curriculum Materials

Objective

Determine different symmetrical tilings of space using the cube as the fundamental domain.

Materials

3-D Tiling Puzzle
Clear Tape Or Glue
Scissors
3/4" Diameter Color Coded Circular Labels

Introduction

From previous activities with 2-dimensional surfaces you learned that gluing opposite edges together of a square in various combinations created surfaces which could be possible universes for a Flatlander. In addition, each gluing creates a symmetrical tiling that demonstrates what one would see as an observer on that surface. In other words, the gluing, the symmetry, and the surface all determine one another. This is also true of 3-dimensional space.

Euclidean 3-space is space that is unbounded and infinite. Can you think of a space that is unbounded and finite? Suppose our universe is a closed space in the same way a Flatland's universe is a closed surface. We can form a closed 3-dimensional universe by gluing opposite faces of a cube together in various combinations. This creates a symmetrical tiling of our motif in the images of it that would be seen from an intrinsic observer's point of view.

Activity 1

Using an overhead transparency with the drawing from the 3-D Tiling Puzzle burned into it, assemble a cube with the figure suspended in the cube's interior. Placing color coded circular labels on the six faces of the cube enhance identifying the front, back, top, bottom, left, and right faces. Repeat the process to assemble eight cubes total. The cube will be the shape we will use as a fundamental domain for the tiling of 3-dimensional Euclidean space and the space ship will be the motif in space.

Activity 2

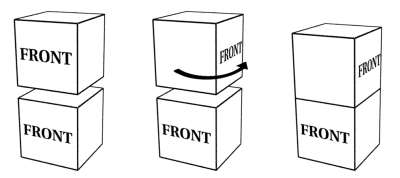
Create the following closed 3-dimensional universe and describe what an observer would see concerning the motif and its moves. Use the eight fundamental domains created in Activity 1 to help you visualize. Create different 3-D tilings with each the following rules:

Attach the front faces to back faces.
Attach the left faces to right faces.
Attach the top faces to bottom faces.
Do both 1 and 2.
Do both 1 and 3.
Do both 2 and 3.
Do all of 1, 2, and 3. (This is called a 3-torus closed universe.)

(To save time, just do 1, 4, and 7 above.)

Activity 3

Create the following closed 3-dimensional universe by adding a "half twist" before gluing as shown in the diagram below. Describe what the an observer would see concerning the motif and its images.


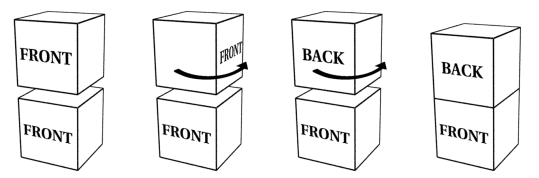Take the cube's top and bottom,	rotate one of them a quarter turn,	rotate it another a quarter turn,	and glue.

Glue front faces to back faces with a half twist.
Glue left faces to right faces with a half twist.
Glue top faces to bottom faces with a half twist.
Do both 1 and 2.
Do both 1 and 3.
Do both 2 and 3.
Do both 1, 2, and 3.

(To save time, just do 1, 4, and 7 above.)

Activity 4

Create the following closed 3-dimensional universe by adding a quarter turn clockwise, from the point of view of the figurine, before gluing as shown in the diagram below. Describe what an observer in this universe would see concerning the motif and its image. Which do not tile space symmetrically?


Take the cube's top and bottom,	rotate one of them a quarter turn,	and glue.

Glue front faces to back face with a quarter turn.
Glue left faces to right face with a quarter turn.
Glue top faces to bottom face with a quarter turn.
Combine 1 and 2.
Combine 1 and 3.
Combine 2 and 3.
Combine 1, 2, and 3.

(To save time, just do 1, 4, and 7 above.)

Questions

Does gluing two opposite faces with a three quarter turn clockwise, from the point of view of the figurine, create a closed 3-dimensional universe that is the same as one created from a quarter turn?
What are other ways of gluing opposite faces together?

Extensions

As a classroom activity, choose any combination of gluing faces and place the cubes from the entire class to tile space in a single stack. Each student takes a turn placing a cube in the stack with the correct orientation. Each student must verify whether the placing of the cube is consistent with the tiling in all directions. What other regular polyhedra will tessellate 3-dimensional space?

Up: The Shape of Space Curriculum Materials: Symmetry and Tiling

The Geometry Center Home Page