4. More on Transformations

Examples of changing transformations

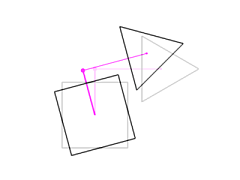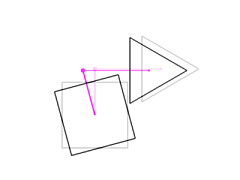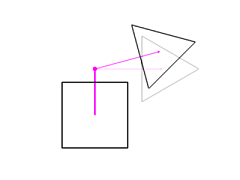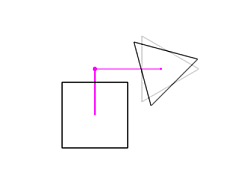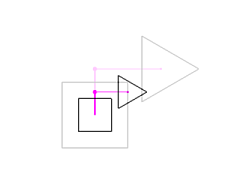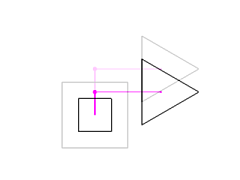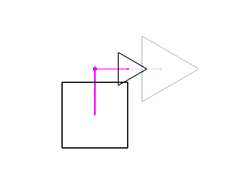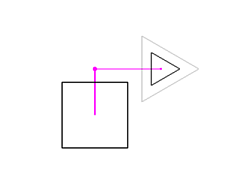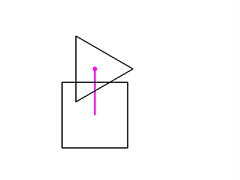
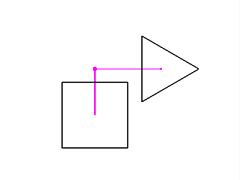
Changing the attachment point to (0, 0.7, 0) moves the triangle up.

Changing the triangle's offset from the attachment point to (1, 0, 0) moves the triangle to the right.

Now we can see what happens when we alter the other transformation properties. If we change the group rotation of the square, we see that everything moves as one piece.

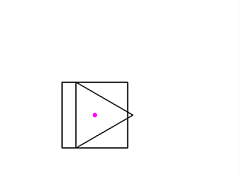
If instead we change just the individual rotation of the square, we see that the triangle's attachment point rotates along with the square, but the triangle itself only translates with the attachment point; it does not rotate.

Changing the triangle's group rotation (shown below on the left) acts about the attachment point. Changing its individual rotation (shown below on the right) acts about its own origin.

Changing the scale is similar to changing the rotation. Changing the box's group scale (shown below on the left) scales everything as one piece. Changing the box's individual scale (shown below on the right) scales the box and the attachment points, but does not change the scale of the triangle.

Changing the triangle's group scale (shown below on the left) is centered at the attachment point. Changing its individual scale (shown below on the right) is centered at its own origin.