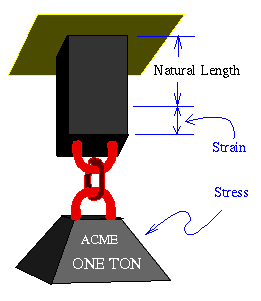
Important mechanical properties of materials can be found tabulated in various engineering handbooks and textbooks. For now, the material property that we will be most interested in is the so-called modulus of elasticity (also called Young's modulus). The modulus of elasticity for a material indicates by how much the material will yield when subjected to a given force per unit area. In technical language, the amount the material yields (elongation per unit length) is called strain , and the force per unit area is called stress .
Many materials change their length approximately linearly in response to an applied force. This response, known as Hooke's Law, is valid when the applied force per unit area is not too great. The ratio of stress to strain is defined to be the modulus of elasticity.
There are a couple of useful ways to think about stress and strain. Suppose our object is a block of rubber. If you think of the stress as pulling on the block, as illustrated below, the strain is how much the block stretches. Alternatively, if you think of the stress as squeezing the block, as would be the case if you put the block in a vise for example, then the stain is the amount the block compresses.

Although the actual stresses and strains in a flexing beam are complicated, it is easy to see how the modulus of elasticity plays a role. If you imagine bending a square beam into an arc, the top edge must stretch and the bottom edge must compress. The more the beam resists stretching and compressing, the harder it will be to bend the beam.

Intuitively, the larger the modulus of elasticity is, then the more rigid the material is. For example, the table below shows that steel is a more rigid material than aluminum or wood, because it has a larger modulus of elasticity. We caution, however, that material properties vary greatly from one sample to the next, and depend on both purity of the sample and the manufacturing process.
It is also important to keep in mind that the modulus of elasticity only describes the behavior of the material for reasonably small stresses where the relation of stress to strain is approximately linear. If you apply enough force, the material will fail in some way. For example, a piece of metal will bend (and not spring back) while wood and concrete will break. Think of pulling apart a plastic bag: once the plastic starts to give way, it stretches very easily. In other words, for just a little more stress, you get a lot more strain, and the modulus of elasticity is no longer meaningful.
The units of the modulus of elasticity (E) are giga-Pascals (10^9 kg/m^2) while the units of density are kg/m^3. In all cases, when a range of values are indicated, we used the greatest values in the software that simulates the bending of beams.
MATERIAL Mod. of Elast.(GPa) Mass Density (kg/m^3) Aluminum Pure 70 2710 Alloys 70-79 2600-2800 Brass 80% Cu, 20% Zn 100 8600 60% Cu, 40% Zn Bronze 96-120 8200-8800 Cast Iron 83-170 7000-7400 Concrete 17-31 2300-2400 Steel 190-210 7850 Stone Granite 40-70 2600 Marble 50-100 2600-2900 Titanium 110 4500 Wood Oak 11-12 640-720 Southern Pine 11-14 560-640 Wrought Iron 190 7400-7800Reference: J.M. Gere and S.P. Timoshenko, Mechanics of Materials , 3rd Ed, PWS-Kent, Boston, 1990.
Copyright © 1996 by The Geometry Center. Last modified: Fri Apr 12 15:51:22 1996