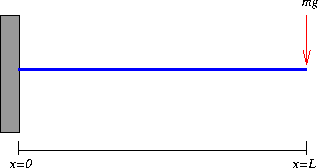
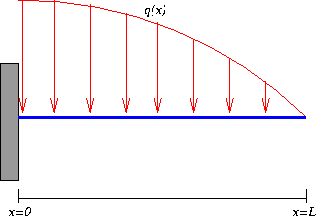
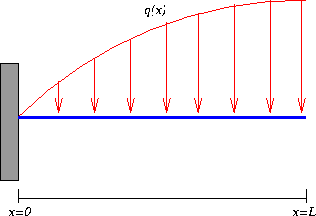
One of the simulations in the interactive portion of this lab is the bending
of a cantilevered beam (i.e. a beam clamped at one end as
pictured below) with a concentrated load placed at x=L (the end of
the beam.)

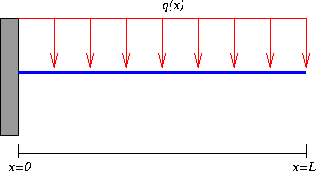
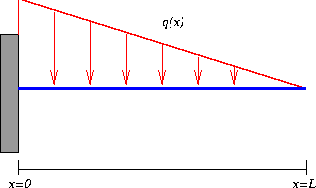
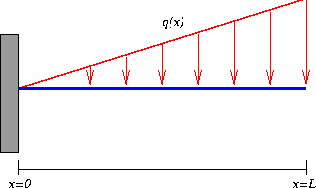
Copyright © 1996 by The Geometry Center. Last modified: Fri Apr 12 15:50:26 1996