How does light travel?
Understanding how and where a rainbow appears is tied to understanding
how light travels. In this section we will investigate some of the
basic theories about the nature of light.
To help with geometric understanding, we will assume that light travels
in rays. We begin with light rays moving through the air at
a constant speed and consider the reflection of light. In
1657 the mathematician
Pierre de Fermat
postulated a simple principle:
Light follows a path that minimizes total travel time.
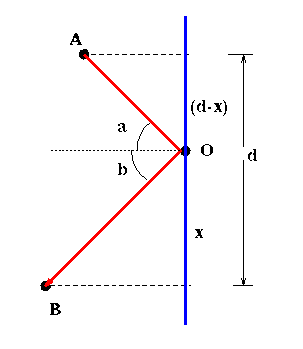
Figure 1: The reflection of light from a smooth surface.
Question 1
Using Fermat's Principle, Figure 1, and
calculus, determine the relationship between the incoming and outgoing
angles.
- Write down an expression for the total
distance that light travels between A and B,
in terms of the unknown position x.
- If we assume that the speed of light through air is a constant,
then distance light travels equals its speed times the time it
takes to travel the distance.
Use calculus and Fermat's Principle to determine an equation that
x must satisfy in order to minimize the time traveled
between A and B.
(You do not need to solve this equation)
- Express the sines of angles a and b in terms
of the side lengths of the triangles in Figure 1.
- Combine the answers to the previous two parts to determine how
sin(a) and sin(b) are related when x
is chosen so as to satisfy Fermat's Principle.
- Argue that this implies that a=b.
Thus you have discovered a relationship between the
angles formed by incoming and outgoing rays of reflected light. We
call a the angle of incidence and
b the angle of reflection. In the last part of Question 1 you
deduced the Law of Reflection: the angle of incidence
is equal to the angle of reflection. It is also possible to
demonstrate the Law of
Reflection completely geometrically.
Next:Refraction
Previous:Objectives
Return to:Outline
Frederick J. Wicklin <fjw@geom.umn.edu>
Paul Edelman <edelman@math.umn.edu>
This lab is based on a module developed by Steven Janke and published
in Modules in Undergraduate Mathematics and its Applications, 1992.
Last modified: Tue Oct 24 15:02:39 1995
