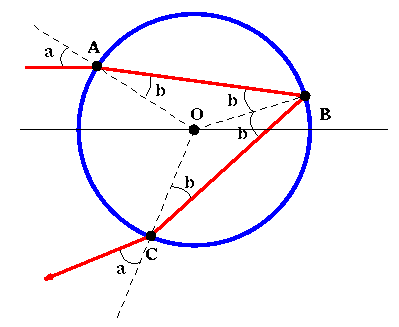
In Figure 4 we depict a light ray hitting a water droplet at point A.
Some of the light will be reflected and some of the light will enter
the droplet. The light that enters will be refracted as discussed in
the previous section. It then hits the other side of the droplet at
point B where some of it will exit and the rest will reflect back.
Finally at point C some of the light will exit and be seen by an
observer.
Experiment #1
For the purpose of the first two experiments, you may ignore
the "wavelength" of light rays. For best "experimental data," set the
"wavelength" to be 700 nanometers (red light). (We will look at the effect of
wavelength later.)
- Graph the deflection angle as a function of the impact parameter for
the impact parameter ranging from 0 to 1 on the
graph provided. (Note: w=0
is the center of the droplet whereas w=1 is the top of
the droplet.)
- Numerically approximate the value of the impact parameter for
which the deflection angle is a minimum (to within an accuracy
of 0.025).
- Note that each value of the impact parameter corresponds to a unique
value of the angle of incidence (a).
What is the value of a that corresponds to the
minimum deflection angle.
Experiment #2
The next activity will help you answer the question "When will incoming
light be focussed most intensely?" In other words, when will a range
of incoming rays all leave the droplet at approximately the same angle?
- Send in 3 incoming beams of light at:
- impact parameters 0.05, 0.1, 0.15
- impact parameters 0.5, 0.55, 0.6
- impact parameters 0.75, 0.8, 0.85
- Sketch the results
- For which set of impact parameters are the outgoing rays the most
concentrated? The most diffuse?
- If an incoming ray has impact parameter w, we define
D(w) to mean the deflected angle of that light ray.
Use the results of the previous experiment to complete
the chart you were given.
Experiment #3
Repeat Experiment #1 with the wavelength of
the incoming light rays set to 400 nanometers (violet light).
- How does the angle of minimum deflection change?
The color of light corresponds to its wavelength. Light with a
wavelength of 400 nanometers is violet; a wavelength of 450 nanometers
is blue. Light with a wavelength of
525 nanometers appears green, 580 nanometers is yellow,
625 nanometers corresponds to orange, and 700 nanometers is red.
- Conjecture how the minimum angle of deflection varies according to
the wavelength of light. Specifically, as the wavelength of light
decreases, does the minimum angle of deflection increase or
decrease? (Make sure your conjecture is supported by your
results from Experiment #1 and the first portion of Experiment #3.)
"White" light is composed of light of all wavelengths. Therefore a
"true" simulation of light passing through a water droplet is to send
in several rays of differing wavelengths at the same
impact parameter and to see how these rays disperse into a rainbow.
Send in 5 incoming beams of light at impact parameters 0.9.
The wavelengths of the incoming beams should be
400, 450, 550, 600, and 700 nanometers.
- What are the corresponding angles of the outgoing rays?
Next: