PARAMETRIC FUNCTIONS (u,v)

The definition of parametric representation is that a surface can be described as images of vector-valued functions. The most common example of a parametric representation in 2 space involves the circle defined as a graph by : x^2+ y^2 = r^2. We can represent the associated disk parametrically by f(u,v) = (ucos v, usin v,0), where u=0..r and v=0..2*Pi.

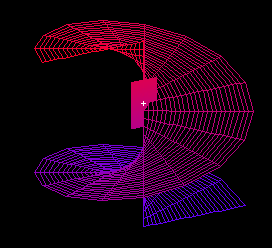
When using a parametric surface, we define the tangent plane to be the plane passing through f(u0,v0) and parallel to the partial derivatives with respect to both u and v. The plane is given parametrically by:

t(s,t) = s(partial w/ respect to u at (u0,v0)) + t(partial w/ respect to v at (u0,v0)) + f(u0,v0)

ex.3

f(u,v) = (ucos v, usin v, v), where u=0..2, and v=0..2*Pi at (u,v) = (1, 2*Pi)

partial of u = (cos v, sinv, 0) = (1, 0, 0)

partial of v = (-usinv, ucos v, 1) = (0, 1, 1)

t(s,t) = s(1, 0, 0) + t(0, 1, 1) + (1, 0, 2*Pi) = (s+1, t, t+2*Pi) for s=-infinity..infinity, t=-infinity..infinity

NOTE: Use the variables s and t in the Maple ParamTan command (ParamTan will not recognize u and v)

QUESTION #2

We define our function to be F(s,t)=(cos(s)cos(t), sin(s)cos(t), sin(t)), s=0..2*Pi, t=0..2*Pi

A. Find the partial derivatives with respect to s and t, and evaluate them at (s0,t0)=(1, 1), our point of interest.

B. These two vectors are the basis vectors for your plane. Turn them into a plane. Hint: this is a vector valued function.

C. Sketch your surface and tangent plane around your point (s0,t0)=(1, 1). You can use maple if you really want to, we allow it. : )

D. Check your answer using the command ParamTan. (If you have not already pasted in the maple code that auxilliary functions, then do so now.) The syntax is as follows:

ParamTan (function defined as 3 vector, s=smin..smax, t=tmin..tmax,point=[s0,t0]);

Note: These are the actual steps that Maple is going through when it calculates the plane.

Next: tangent planes to implicitly defined surfaces

Back: tangent planes to graphs