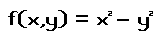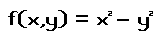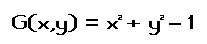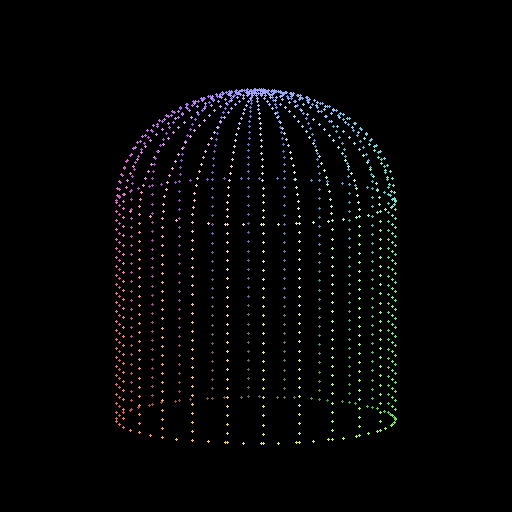Applications of Lagrange multipliers

There are many cool applications for the Lagrange multiplier method. For example, we will show you how to find the extrema on the world famous Pringle surface. The Pringle surface can be given by the equation

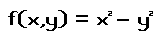
Let us bound this surface by the unit circle, giving us a very happy pringle. :) In this case, the boundary would be

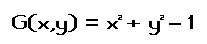
The first step is to find the extrema on an unbounded f.

Question 1

What is the gradient of f(x,y)?
What are the extrema of an unbounded f?
Is/are the point(s) you have found maxima, minima, or saddle points?

There are sure to be more extrema on the bounded surface then the one(s) you have just found. These are quite simple to find; they are given by grad(f(x,y) + a*grad(G(x,y)) = 0.

Question 2

Find the above expression.
Find the points along G(x,y) where the above expression is true.
Is/are the point(s) you have found maxima, minima, or none of the above?

Here is the command to graph the Pringle surface and its boundary, the unit circle:

plots[display3d]({plot3d(2*x^2-2*y^2, x=-1.2..1.2, y=-1.2..1.2), plots[spacecurve]([cos (t), sin (t), 2*(cos (t))^2-2*(sin (t))^2], t=0..2*Pi), plots[spacecurve]([cos (t), sin (t), -5], t=0..2*Pi)},style=WIREFRAME);

You may wish to experiment with this graph; for example, you might wish to consider rotating the graph or looking at different styles.

Besides just the pure mathematical examples such as the one you have just done, there are a plethora of practical examples of how Lagrange multipliers can be used. For the next example, you will be exploring the most efficient way to build a silo. We will be looking at two different situations of this. In the first example, you will be attempting to minimize the surface area of a silo with a volume of 1000 cubic meters.

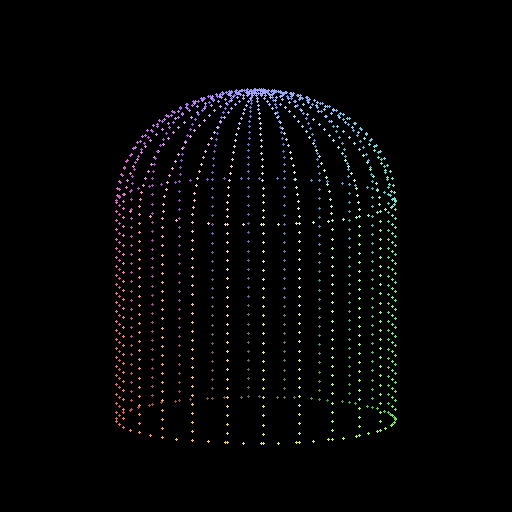
The silo is essentially a cylinder with a half sphere on top; let the cylinder have height h and let the cylinder and sphere have radius r.

Question 3

Find functions for the volume and the surface area of the silo.
Using the Lagrange multiplier method, find the dimensions such that the surface area is minimized for the given volume. In this case, F is the surface area function.
Do these dimensions seem reasonable? Why?

Next, we will look at the cost of building a silo of volume 1000 cubic meters. The curved surface on top of the silo costs $3 per square meter to build, while the walls cost $1 per square meter.

Question 4

Set up equations for the volume and the cost of building the silo.
Using the Lagrange multiplier method, find the cheapest way to buld the silo.
Do these dimensions seem reasonable? Why?

Of course, if all situations were this simple, there would be no need for the Lagrange multiplier method, since there are other methods for solving 2 variable functions that are much nicer. However, with a greater number number of variables, the Lagrange multiplier method is much more fun.

For the next example, imagine you are working at the State Fair (since you're so desperate for money that you can't even buy a bagel anymore). You find yourself at the snowcone booth, and your boss, upon hearing that you are good at math, offers you a bonus if you can design the most efficient snowcone. You assume the snowcone will be modelled by a half-ellipsoid perched upon a cone.

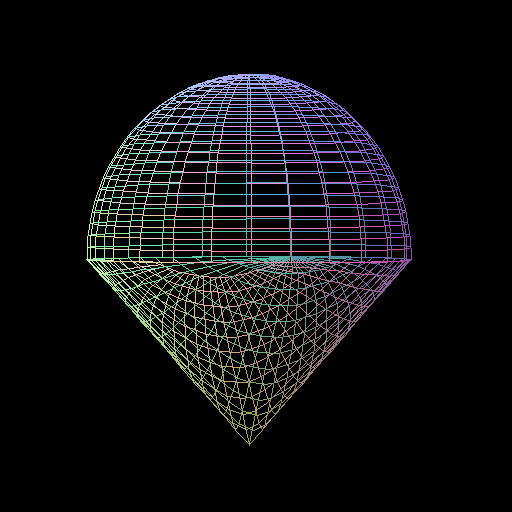
Your boss only wants to use 84 square centimeters of paper per cone, and wants to have it hold the maximum amount of snow. This can be represented in 3 variables: r (the radius of the cone), h (the height of the cone), and s (the height of the half-ellipsoid). In order to keep the snow from tumbling off the cone, s cannot be greater than 1.5*r. We have provided hints for the equations if you need them.

Question 5

Use the Lagrange multiplier method to find the most efficient method. Be sure to check all boundaries.
Is this a reasonable design?
If it is, explain why; if it isn't, give parameters that might make it seem reasonable.

Previous: What Lagrange Multipliers are, and what they are good for.

Next: Conclusion.