The Evolute
Remember curvature? For a parametric function defined in terms of x(t) and y(t) cuvature, k, is 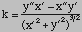 . Curvature tells us
how fast the curve is moving away from the tangent line. There is also a center
of curvature. This is the center of the circle that best models the curve at
a point. This circle has a radius r which is called the radius of curvature.
. Curvature tells us
how fast the curve is moving away from the tangent line. There is also a center
of curvature. This is the center of the circle that best models the curve at
a point. This circle has a radius r which is called the radius of curvature.
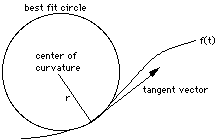 The length of r = 1/k, where k is the curvature.
The length of r = 1/k, where k is the curvature.
If we plot the center of curvature for every point on a curve we get a second curve.
This curve is called the evolute. As long as the curve is continuously differentiable the curvature is a continuous function.
Question 2:
Under what circumstances is the radius of curvature not defined?
Now let's try applying the evolute to some of the cycloids we looked at before.
First let's look at the linear cycloids we looked at in the first section of this
lab. Try looking at examples where
| a | < | b |, | a | = | b |, and | a | > | b |. We
suggest looking at (a, b) = (1, 2), (1, 1), (2, 1). To use the evolute function you
must
read in the Maple code. After you have defined
x and y you can type in plot(evolute4(x, y, 0, 8*Pi), scaling=constrained); to create a plot of the original curve and its evolute.
Question 3:
a. From looking at these graphs, what do local extrema in the y direction
on the original curve correspond to on the curve of the evolute?
b. What happens when | a | = | b |?
c. What happens when | a | > | b |? Can you explain this by looking at the
shape of the original curve? What is happening? (Hint: Think about best fit circles.)
[Back] [Next Page]
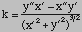 . Curvature tells us
how fast the curve is moving away from the tangent line. There is also a center
of curvature. This is the center of the circle that best models the curve at
a point. This circle has a radius r which is called the radius of curvature.
. Curvature tells us
how fast the curve is moving away from the tangent line. There is also a center
of curvature. This is the center of the circle that best models the curve at
a point. This circle has a radius r which is called the radius of curvature.
 The length of r = 1/k, where k is the curvature.
The length of r = 1/k, where k is the curvature.