Glossary



Next: Background for Further
Up: Interactive Methods for Visualizable
Previous: References
- Manifold- A generalization of
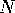 -dimensional space
in which a neighborhood of each point, called its chart, looks
like Euclidean space. The charts are related to
each other by Cartesian coordinate transformations and comprise
an atlas for the manifold. The atlas may be non-trivially
connected; there are round-trip tours of a manifold that cannot
be contracted to a point. The surface of a donut, called a torus, is a familiar non-trivial 2D manifold.
-dimensional space
in which a neighborhood of each point, called its chart, looks
like Euclidean space. The charts are related to
each other by Cartesian coordinate transformations and comprise
an atlas for the manifold. The atlas may be non-trivially
connected; there are round-trip tours of a manifold that cannot
be contracted to a point. The surface of a donut, called a torus, is a familiar non-trivial 2D manifold.
- Submanifold, ambient space.
A submanifold is a subset of a manifold,
its ambient space, for which each point
has a chart in which the submanifold looks
like a linear subspace of lower dimension.
A common knot is a 1-dimensional submanifold of its
3-dimensional ambient space.
- Homotopy. A continuous deformation of a mathematical object
which preserves its topological integrity but may develop
self-intersections and even worse singularities. There is a
homotopy that takes a teapot to a torus (a sphere with a hole).
There is another deforming it to a point.
- Isotopy. A homotopy of an object produced by a deformation
of the ambient space, so therefore the object cannot develop
new self-intersections. The deformation of the teapot
to a torus is an isotopy, but the deformation to a point is not.
- Embedding. The parametrization of a submanifold
by means of a standard model. A knotted sphere
in 4-space is an embedding of the familiar round sphere.
Whitney's theorem says that an
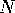 -dimensional manifold is
guaranteed to have an embedding in Euclidean
-dimensional manifold is
guaranteed to have an embedding in Euclidean 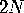 -space.
-space.
- Immersion. A locally (but not globally) smoothly invertible
mapping of one manifold into another. The image may have
self-intersections; the figure-8 is an immersion of the circle in 2D.
- Minimal Surface. A surface that locally has the
smallest area given a particular topological shape for it, and
possibly, constrained by a fixed boundary (soap-films) or
prescribed behavior at infinity.
- Steepest Descent Method. A particular way of guiding
an isotopy of an embedded surface to one which minimizes a
function that measures its shape. Moving down the gradient of
the area function often terminates at a minimal surface.



Next: Background for Further
Up: Interactive Methods for Visualizable
Previous: References
Tamara Munzner
Thu Sep 21 19:17:33 CDT 1995
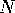 -dimensional space
in which a neighborhood of each point, called its chart, looks
like Euclidean space. The charts are related to
each other by Cartesian coordinate transformations and comprise
an atlas for the manifold. The atlas may be non-trivially
connected; there are round-trip tours of a manifold that cannot
be contracted to a point. The surface of a donut, called a torus, is a familiar non-trivial 2D manifold.
-dimensional space
in which a neighborhood of each point, called its chart, looks
like Euclidean space. The charts are related to
each other by Cartesian coordinate transformations and comprise
an atlas for the manifold. The atlas may be non-trivially
connected; there are round-trip tours of a manifold that cannot
be contracted to a point. The surface of a donut, called a torus, is a familiar non-trivial 2D manifold.
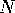 -dimensional manifold is
guaranteed to have an embedding in Euclidean
-dimensional manifold is
guaranteed to have an embedding in Euclidean 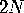 -space.
-space.