Introduction



Next: Pictures and Mathematics
Up: Interactive Methods for Visualizable
Previous: Interactive Methods for Visualizable
Mathematical visualization is the art of creating a tangible
experience with abstract mathematical objects and concepts. While this
process has been a cornerstone of the mathematical reasoning process
since the times of the ancient geometers, the advent of high-performance
interactive computer graphics systems
has opened a new era whose ultimate significance can only be imagined.
Typical geometric problems of interest to mathematical
visualization applications involve both static structures, such as
real or complex manifolds, and changing structures requiring
animation.
In practice, the emphasis is on manifolds of dimension two or three
embedded in three or four-dimensional spaces
due to the practical limitations of holistic human spatial perception
- it is extremely challenging to construct intuitively useful images
of anything more complicated!
General approaches to
visualizing 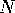 -dimensional spaces
are at best piecemeal,
so that algebraic
manipulations often remain our most powerful tool for high dimensions.
Nevertheless, despite the apparent
limitations of visual representations, their utility
is far from being completely exploited;
we may still gain significant
intuitive value by pushing our visual understanding of
relatively simple geometric objects as far as our imagination
can take us.
-dimensional spaces
are at best piecemeal,
so that algebraic
manipulations often remain our most powerful tool for high dimensions.
Nevertheless, despite the apparent
limitations of visual representations, their utility
is far from being completely exploited;
we may still gain significant
intuitive value by pushing our visual understanding of
relatively simple geometric objects as far as our imagination
can take us.
Our goal is to show the nature of the interrelationship between
mathematics and computer science, especially computer graphics.
In this article, we adopt for the most part a computer scientist's
perspective on the progress, techniques, and prospects of mathematical
visualization, emphasizing those areas of 3D and 4D geometry where
interactive paradigms are of growing importance. Without demanding
detailed mathematical expertise of the reader, we present a selection
of the domains with which we are familiar, describe some of the
critical visualization problems involved, and discuss how various
researchers have approached the solution of these problems.
The article begins with some general background and then turns its
attention to some of the visualization methods that have been used to
bring computer graphics technology to bear on mathematical problems of
low-dimensional topology and geometry. The concluding sections
discuss the system design philosophies of various research groups
and prospects for the future.
Examples of computer-generated
images are supplied throughout, and separate sidebars are devoted to a
brief glossary, sources of additional background information
on visualizable mathematics, and an overview of
selected
film and video animations concerned with mathematical
visualization.



Next: Pictures and Mathematics
Up: Interactive Methods for Visualizable
Previous: Interactive Methods for Visualizable
Tamara Munzner
Thu Sep 21 19:17:33 CDT 1995
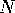 -dimensional spaces
are at best piecemeal,
so that algebraic
manipulations often remain our most powerful tool for high dimensions.
Nevertheless, despite the apparent
limitations of visual representations, their utility
is far from being completely exploited;
we may still gain significant
intuitive value by pushing our visual understanding of
relatively simple geometric objects as far as our imagination
can take us.
-dimensional spaces
are at best piecemeal,
so that algebraic
manipulations often remain our most powerful tool for high dimensions.
Nevertheless, despite the apparent
limitations of visual representations, their utility
is far from being completely exploited;
we may still gain significant
intuitive value by pushing our visual understanding of
relatively simple geometric objects as far as our imagination
can take us.