 +b
+b +c
+c =1 and d
=1 and d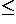 0 in the equation
ax+by+cz+d=0, the
equation is said to be in normal form. In this case d is the
distance of the plane to the origin, and (a,b,c) are the
direction cosines of the normal.
0 in the equation
ax+by+cz+d=0, the
equation is said to be in normal form. In this case d is the
distance of the plane to the origin, and (a,b,c) are the
direction cosines of the normal.
Next: 12.3 Lines
Up: 12 DirectionsPlanes and Lines
Previous: 12.1 Direction Angles and Direction Cosines
The (cartesian) equation of a plane is linear in the coordinates x and y, that is, of the form ax+by+cz+d=0. The normal direction to this plane is (a,b,c). The intersection of this plane with the x-axis, or x-intercept, is x=-d/a; the y-intercept is y=-d/b, and the z-intercept is z=-d/c. The plane is vertical (perpendicular to the xy-plane) if c=0; it is perpendicular to the x-axis if b=c=0; and likewise for the other coordinates.
When a +b
+b +c
+c =1 and d
=1 and d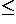 0 in the equation
ax+by+cz+d=0, the
equation is said to be in normal form. In this case d is the
distance of the plane to the origin, and (a,b,c) are the
direction cosines of the normal.
0 in the equation
ax+by+cz+d=0, the
equation is said to be in normal form. In this case d is the
distance of the plane to the origin, and (a,b,c) are the
direction cosines of the normal.
To reduce an arbitrary equation
ax+by+cz+d=0
to normal form, divide by
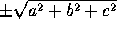 , where the sign of the radical is chosen opposite
the sign of d when d
, where the sign of the radical is chosen opposite
the sign of d when d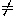 0, the same as the sign of c when
d=0 and c
0, the same as the sign of c when
d=0 and c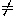 0, and the same as the sign of b otherwise.
0, and the same as the sign of b otherwise.
Plane through (x ,y
,y ,z
,z ) and perpendicular to the direction (a,b,c):
) and perpendicular to the direction (a,b,c):
a(x-x )+b(y-y
)+b(y-y )+c(z-z
)+c(z-z )=0
)=0
Plane through (x ,y
,y ,z
,z ) and
parallel to the directions (a
) and
parallel to the directions (a ,b
,b ,c
,c ) and (a
) and (a ,b
,b ,c
,c ):
):
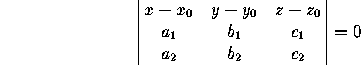
Plane through (x ,y
,y ,z
,z ) and
(x
) and
(x ,y
,y ,z
,z ) and
parallel to the direction (a,b,c):
) and
parallel to the direction (a,b,c):
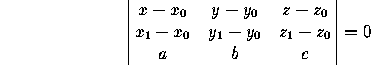
Plane going through (x ,y
,y ,z
,z ),
(x
),
(x ,y
,y ,z
,z ) and
(x
) and
(x ,y
,y ,z
,z ):
):
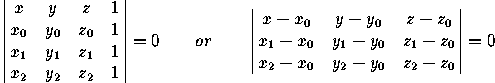
(The last three formulas remain true in oblique coordinates.)
The distance from the point (x ,y
,y ,z
,z ) to the plane
ax+by+cz+d=0 is
) to the plane
ax+by+cz+d=0 is
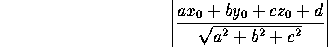
The angle between two planes a x+b
x+b y+c
y+c z+d
z+d =0 and
a
=0 and
a x+b
x+b y+c
y+c z+d
z+d =0 is
=0 is
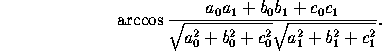
In particular, the two planes are parallel when a :b
:b :c
:c =
a
=
a :b
:b :c
:c , and perpendicular when a
, and perpendicular when a a
a +b
+b b
b +c
+c c
c =0.
=0.
Four planes a x+b
x+b y+c
y+c z+d
z+d =0,
a
=0,
a x+b
x+b y+c
y+c z+d
z+d =0,
a
=0,
a x+b
x+b y+c
y+c z+d
z+d =0 and
a
=0 and
a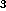 x+b
x+b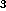 y+c
y+c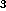 z+d
z+d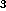 =0 are concurrent if and
only if
=0 are concurrent if and
only if
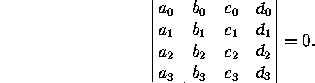
Four points (x ,y
,y ,z
,z ),
(x
),
(x ,y
,y ,z
,z ), (x
), (x ,y
,y ,z
,z )
and (x
)
and (x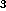 ,y
,y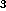 ,z
,z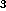 )
are
coplanar if and only if
)
are
coplanar if and only if
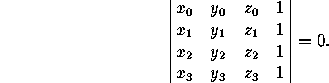
(Both of these assertions remain true in oblique coordinates.)
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.