Next: 12 DirectionsPlanes and Lines
Up: 11 Other Transformations of Space
Previous: 11.2 Affine Transformations
A transformation that maps lines to lines (but does not necessarily
preserve parallelism) is a projective transformation. Any
spatial projective transformation can be expressed by an invertible
4×4 matrix in homogeneous coordinates; conversely, any
invertible 4×4 matrix defines a projective transformation of
the plane. Projective transformations (if not affine) are not defined
on all of space, but only on the complement of a plane (the missing
plane is ``mapped to infinity'').
The following particular case is often useful, especially in computer
graphics, in projecting a scene from space to the plane. Suppose
an observer is at the point E=(x ,y
,y ,z
,z ) of space, looking toward
the origin O=(0,0,0). Let P, the screen, be the plane
through O and perpendicular to the ray EO. Place a rectangular
coordinate system
) of space, looking toward
the origin O=(0,0,0). Let P, the screen, be the plane
through O and perpendicular to the ray EO. Place a rectangular
coordinate system 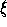
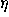 on P with origin at O and such that
the positive
on P with origin at O and such that
the positive 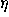 -axis lies in the half-plane determined by E and
the positive z-axis of space (that is, the z-axis is pointing
``up'' as seen from E). Then consider the transformation that
associates to a point X=(x,y,z) the triple (
-axis lies in the half-plane determined by E and
the positive z-axis of space (that is, the z-axis is pointing
``up'' as seen from E). Then consider the transformation that
associates to a point X=(x,y,z) the triple (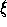 ,
,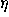 ,
,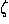 ), where
(
), where
(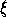 ,
,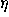 ) are the coordinates of the point where the line EX
intersects P (the screen coordinates of X as seen from E),
and
) are the coordinates of the point where the line EX
intersects P (the screen coordinates of X as seen from E),
and 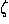 is the inverse of the signed distance from X to E
along the line EO (the depth of X as seen from E). This is
a projective transformation, given by the matrix
is the inverse of the signed distance from X to E
along the line EO (the depth of X as seen from E). This is
a projective transformation, given by the matrix
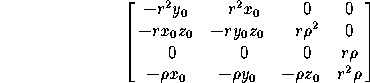
with 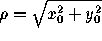 and
and 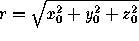 .
.
Next: 12 DirectionsPlanes and Lines
Up: 11 Other Transformations of Space
Previous: 11.2 Affine Transformations
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.
 ,y
,y ,z
,z ) of space, looking toward
the origin O=(0,0,0). Let P, the screen, be the plane
through O and perpendicular to the ray EO. Place a rectangular
coordinate system
) of space, looking toward
the origin O=(0,0,0). Let P, the screen, be the plane
through O and perpendicular to the ray EO. Place a rectangular
coordinate system 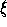
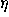 on P with origin at O and such that
the positive
on P with origin at O and such that
the positive 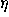 -axis lies in the half-plane determined by E and
the positive z-axis of space (that is, the z-axis is pointing
``up'' as seen from E). Then consider the transformation that
associates to a point X=(x,y,z) the triple (
-axis lies in the half-plane determined by E and
the positive z-axis of space (that is, the z-axis is pointing
``up'' as seen from E). Then consider the transformation that
associates to a point X=(x,y,z) the triple (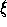 ,
,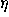 ,
,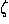 ), where
(
), where
(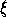 ,
,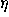 ) are the coordinates of the point where the line EX
intersects P (the screen coordinates of X as seen from E),
and
) are the coordinates of the point where the line EX
intersects P (the screen coordinates of X as seen from E),
and 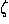 is the inverse of the signed distance from X to E
along the line EO (the depth of X as seen from E). This is
a projective transformation, given by the matrix
is the inverse of the signed distance from X to E
along the line EO (the depth of X as seen from E). This is
a projective transformation, given by the matrix
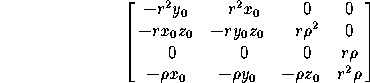
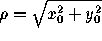 and
and 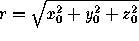 .
.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page