 (ax,ay,az),
(ax,ay,az),
Next: 11.2 Affine Transformations
Up: 11 Other Transformations of Space
Previous: 11 Other Transformations of Space
A transformation of space that preserves shapes is called a similarity. Every similarity of the plane is obtained by composing a proportional scaling transformation (also known as a homothety) with an isometry. A proportional scaling transformation centered at the origin has the form
(x,y,z) (ax,ay,az),
(ax,ay,az),
where a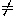 0 is the scaling factor (a real number).
The corresponding matrix in homogeneous coordinates is
0 is the scaling factor (a real number).
The corresponding matrix in homogeneous coordinates is
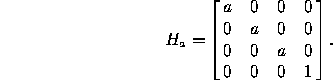
In cylindrical coordinates, the transformation is
(r, ,z)
,z)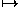 (ar,
(ar, ,az).
,az).
In spherical coordinates, it is
(r, ,
, )
)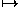 (ar,
(ar, ,
, ).
).
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.