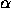 around a line L;
around a line L;
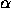 around a line L, with
displacement d;
around a line L, with
displacement d;
Next: 10.1 Formulas for Symmetries in Cartesian Coordinates
Up: Part II: Three-Dimensional Geometry
Previous: 9.5 Homogeneous Coordinates in Space
A transformation of space (invertible map of the plane to itself) that preserves distances is called an isometry of space. Every isometry of space is of one of the following types:
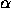 around a line L;
around a line L;
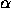 around a line L, with
displacement d;
around a line L, with
displacement d;
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.