
Next: Part II: Three-Dimensional Geometry
Up: 8 Special Plane Curves
Previous: 8.3 Spirals
There are examples of curves (in the sense of continuous maps from the real line to the plane) that completely cover a two-dimensional region of the plane. We give a construction of such a Peano curve, adapted from David Hilbert's example. The construction is inductive, and is based on replacement rules. We consider building blocks of six shapes,

the length of the straight pieces being twice the radius of the curved ones. A sequence of these patterns end-to-end represents a curve, if we disregard the red and green half-disks. The replacement rules are the following:
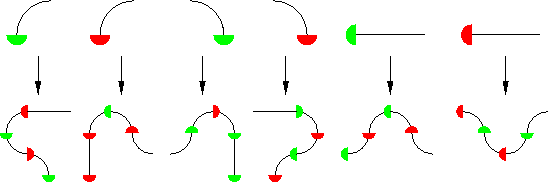
The rules are applied taking into account the way each piece is turned. Here we apply the replacement rules to a particular initial pattern:
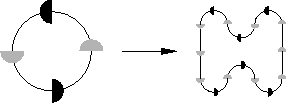
(We scale the result so it has the same size as the original.) Applying the process repeatedly gives, in the limit, the Peano curve. Here are the first five steps:

The same idea of replacement rules leads to many interesting fractal,
and often self-similar, curves. For example, the substitution
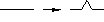 leads to the
Koch snowflake when applied to an initial equilateral triangle,
like this (the first three stages and the sixth are shown):
leads to the
Koch snowflake when applied to an initial equilateral triangle,
like this (the first three stages and the sixth are shown):

![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.