 ,y
,y ) and (x
) and (x ,y
,y ), this distance
is
), this distance
is
Next: 4.2 Angles
Up: 4 Lines
Previous: 4 Lines
The distance between two points in the plane is the length
of the line segment joining the two points. If the points have
cartesian coordinates (x ,y
,y ) and (x
) and (x ,y
,y ), this distance
is
), this distance
is
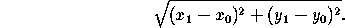
If the points have polar coordinates (r ,
,
 ) and
(r
) and
(r ,
,
 ), this distance is
), this distance is
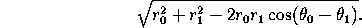
If the points have oblique coordinates (x ,y
,y ) and
(x
) and
(x ,y
,y ), this distance is
), this distance is
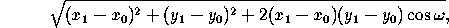
where 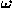 is the angle between the axes (Figure 1.5.1
).
is the angle between the axes (Figure 1.5.1
).
The point k% of the way from P =(x
=(x ,y
,y ) to P
) to P =(x
=(x ,y
,y ) is
) is
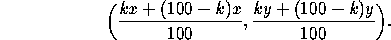
(The same formula works also in oblique coordinates.) This point
divides the segment P P
P in the ratio k:(100-k). As a
particular case, the midpoint of P
in the ratio k:(100-k). As a
particular case, the midpoint of P P
P is given by
is given by
(½(x +x
+x ), ½(y
), ½(y +y
+y )).
)).
The distance from the point (x ,y
,y ) to the line ax+by+c=0 is
) to the line ax+by+c=0 is

![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.