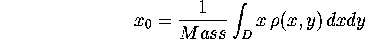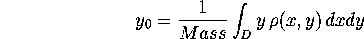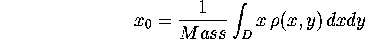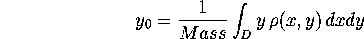Integrating Density Distributions

If we think about balancing a thin book or a uniform plate on one finger, then it is clear that there is some point (called the centroid or center of mass) that represents the center of the object. For symmetric objects (e.g. a circular plate or a rectangular book) which have uniform density, the center of mass is easy to find.

For irregularly shaped objects, or for objects with varying density, the center of mass is much harder to find.

Mathematically, if the density (p) of a flat object is given, we can find the total mass by integrating the density over the region, D. The centroid (x0,y0) of the region D is found by integrating related functions:

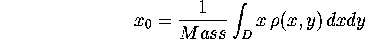
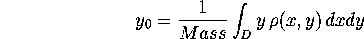
Question #4

Assume that the density of Minnesota is a constant 1. Approximate the mass of the state:
density:=1; mass:=evalf(MNleftbox(density,grid=[20,20]));
Now approximate the center of mass:
x0:=1/mass*evalf(MNleftbox(x*density,grid=[20,20])); y0:=1/mass*evalf(MNleftbox(y*density,grid=[20,20]));
Indicate this point on the map of Minnesota that you were given.

Question #5

In actuality, the density of Minnesota is very hard to model. One of the features of the state that is worth modelling is the so-called Iron Range, in northern Minnesota. This strip of land contains iron ore and so we might expect the average density of rock in this area to be greater than the state average.

Assume that the density of Minnesota is modelled by
density:=1+2/5*E^(-1/2*(y-x/4-10)^2);

Use the plot3D command to plot the density function for x=-1.5..14, y=0..16 (You may wish to set scaling=CONSTRAINED and color-code the function by height (shading=ZHUE)).
Compute the new mass and center of mass and indicate this new point on the map. How did the center of mass shift?

Question #6

Now consider where Minnesota would balance in terms of its population distribution. There are more people in the south than in the north, and there are more people in the east (the Twin Cities, Duluth, Rochester) than in the west.

We will model the population density of Minnesota by the function
density:=1-y/30+2*E^(-(x-1/10*(y-5)^2-6.5)^2);

Use the plot3D command to view the density.
Compute the center of population mass and indicate this point on the map.

Up: Introduction
Previous: Convergence of Area

Frederick J. Wicklin <fjw@geom.umn.edu>

Brian Burt<burt@geom.umn.edu>

Document Created: Fri Jan 27 CST
Last modified: Fri Feb 3 11:56:22 1995