The Euler characteristic of an orbifold
Next: Positive and negative
Up: Geometry and the Imagination
Previous: The orbifold shop
Suppose we have a symmetric pattern in the plane. We can make a symmetric
map by subdividing the quotient orbifold into polygons, and then `unrolling
it' or `unfolding it' to get a map in the plane.
If we look at a large area 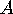 in the plane, made up from
in the plane, made up from 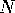 copies of a
fundamental domain, then each face in the map on the quotient orbifold
contributes
copies of a
fundamental domain, then each face in the map on the quotient orbifold
contributes 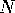 faces to the region. An edge which is not on a mirror
also contributes approximately
faces to the region. An edge which is not on a mirror
also contributes approximately 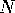 copies - approximately, because when
it is on the boundary of
copies - approximately, because when
it is on the boundary of 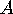 , we don't quite know how to match
it with a fundametnal region.
, we don't quite know how to match
it with a fundametnal region.
In general, if an edge or point has order 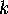 symmetry which
which preserves it, it contributes approximately
symmetry which
which preserves it, it contributes approximately 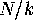 copies of
itself to
copies of
itself to 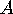 , since each time it occurs, as long as it is not on
the boundary of
, since each time it occurs, as long as it is not on
the boundary of 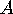 , it is counted in
, it is counted in 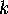 copies of the fundamental domain.
copies of the fundamental domain.
Thus,
-
If an edge is on a mirror, it contributes only approximately
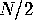 copies.
copies.
-
If a vertex is not on a mirror and not on a cone point, it contributes
approximately
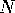 vertices to
vertices to 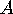 .
.
-
If a vertex is on a cone point of order
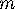 it contributes approximately
it contributes approximately 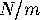 vertices.
vertices.
-
If a vertex is on a mirror but not on a corner reflector, it contributes
approximately
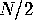 .
.
-
If a vertex is on an order
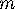 corner reflector, it contributes
approximately
corner reflector, it contributes
approximately 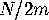
Question.
Can you justify the use of `approximately' in the list above?
Take the area 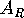 to be the union of
all vertices, edges, and faces that intersect a disk of radius
to be the union of
all vertices, edges, and faces that intersect a disk of radius 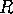 in the plane, along with all edges of any face that intersects and
all vertices of any edge that intersects. Can you show that the
ratio of the true number to the estimated number is arbitrarily close
to 1, for
in the plane, along with all edges of any face that intersects and
all vertices of any edge that intersects. Can you show that the
ratio of the true number to the estimated number is arbitrarily close
to 1, for 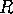 high enough?
high enough?
Definition.
The orbifold Euler characteristic is 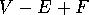 , where each
vertex and edge is given weight
, where each
vertex and edge is given weight 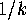 , where
, where 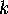 is the order of symmetry
which preserves it.
is the order of symmetry
which preserves it.
It is important to keep in mind the distinction between the topological
Euler characteristic and the orbifold Euler characteristic. For instance,
consider the billiard table orbifold, which is just a rectangle.
In the orbifold Euler characteristic,
the four corners each count 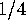 , the four edges count
, the four edges count 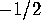 , and the
face counts 1, for a total of 0. In contrast, the
topological Euler characteristic
is
, and the
face counts 1, for a total of 0. In contrast, the
topological Euler characteristic
is 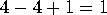 .
.
Theorem.
The quotient orbifold of for any symmetry pattern in the Euclidean plane
which has a bounded fundamental region has orbifold Euler number 0.
Sketch of proof: take a large area in the plane that is topologically
a disk. Its Euler characteristic is 1. This is approximately
equal to 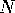 times the orbifold Euler characteristic, for some large
times the orbifold Euler characteristic, for some large 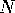 ,
so the orbifold Euler characteristic must be 0.
,
so the orbifold Euler characteristic must be 0.
How do the people at The Orbifold Shop figure its prices?
The cost is based on the orbifold Euler characteristic: it costs
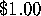 to lower the orbifold Euler characteristic by 1.
When they install a fancy new part, they calculate the difference between
the new part and the part that was traded in.
to lower the orbifold Euler characteristic by 1.
When they install a fancy new part, they calculate the difference between
the new part and the part that was traded in.
For instance, to install
a cone point, they remove an ordinary point. An ordinary point counts 1,
while an order 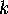 cone point counts
cone point counts 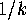 , so the difference is
, so the difference is 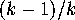 .
.
To install a handle, they arrange a map on the original orbifold so that it
has a square face. They remove the square, and identify opposite edges
of it. This identifies all four vertices to a single vertex. The net
effect is to remove 1 face, remove 2 edges (since 4 are reduced to 2),
and to remove 3 vertices. The effect on the orbifold Euler characteristic
is to subtract 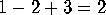 , so the cost is
, so the cost is 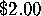 .
.
Question.
Check the validity of the costs charged by The Orbifold Shop
for the other parts of an orbifold.
To complete the connection between orbifold Euler characteristic and
symmetry patterns, we would have to verify that each of the possible
configurations of parts with orbifold Euler characteristic 0 actually
does come from a symmetry pattern in the plane. This can be done in
a straightforward way by explicit constructions. It is illuminating
to see a few representative examples, but it is not very illuminating
to see the entire exercise unless you go through it yourself.
Next: Positive and negative
Up: Geometry and the Imagination
Previous: The orbifold shop
Peter Doyle
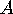 in the plane, made up from
in the plane, made up from 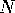 copies of a
fundamental domain, then each face in the map on the quotient orbifold
contributes
copies of a
fundamental domain, then each face in the map on the quotient orbifold
contributes 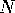 faces to the region. An edge which is not on a mirror
also contributes approximately
faces to the region. An edge which is not on a mirror
also contributes approximately 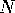 copies - approximately, because when
it is on the boundary of
copies - approximately, because when
it is on the boundary of 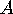 , we don't quite know how to match
it with a fundametnal region.
, we don't quite know how to match
it with a fundametnal region.
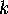 symmetry which
which preserves it, it contributes approximately
symmetry which
which preserves it, it contributes approximately 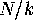 copies of
itself to
copies of
itself to 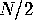 copies.
copies.
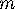 it contributes approximately
it contributes approximately 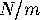 vertices.
vertices.
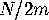
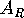 to be the union of
all vertices, edges, and faces that intersect a disk of radius
to be the union of
all vertices, edges, and faces that intersect a disk of radius 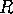 in the plane, along with all edges of any face that intersects and
all vertices of any edge that intersects. Can you show that the
ratio of the true number to the estimated number is arbitrarily close
to 1, for
in the plane, along with all edges of any face that intersects and
all vertices of any edge that intersects. Can you show that the
ratio of the true number to the estimated number is arbitrarily close
to 1, for 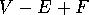 , where each
vertex and edge is given weight
, where each
vertex and edge is given weight 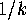 , where
, where 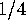 , the four edges count
, the four edges count 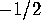 , and the
face counts 1, for a total of 0. In contrast, the
topological Euler characteristic
is
, and the
face counts 1, for a total of 0. In contrast, the
topological Euler characteristic
is 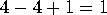 .
.
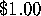 to lower the orbifold Euler characteristic by 1.
When they install a fancy new part, they calculate the difference between
the new part and the part that was traded in.
to lower the orbifold Euler characteristic by 1.
When they install a fancy new part, they calculate the difference between
the new part and the part that was traded in.
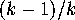 .
.
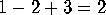 , so the cost is
, so the cost is 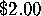 .
.