Surfaces
Next: How to knit
Up: Geometry and the Imagination
Previous: Topology
A surface, or 2-manifold,
is a shape any small enough neighborhood of which
is topologically equivalent to a neighborhood of a point in the plane.
For instance, a the surface of a cube is a surface topologically
equivalent to the surface of a sphere.
On the other hand, if we put an extra wall inside a cube dividing it
into two rooms, we no longer have a surface, because there are points
at which three sheets come together. No small neighborhood of those
points is topologically equivalent to a small neighborhood in the plane.
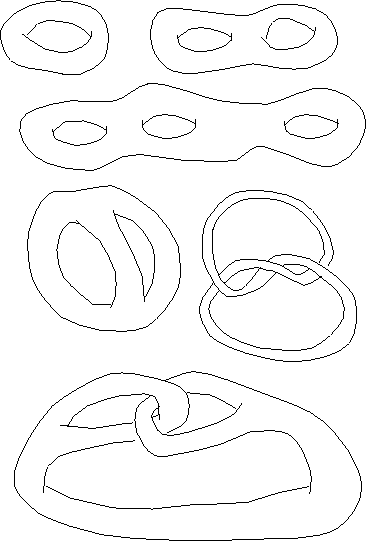
Figure 7: Here are some pictures of surfaces. The
pictures are intended to indicate things like doughnuts and pretzels rather than flat strips of paper.
Can you identify these surfaces, topologically? Which ones are topologically
the same intrinsically, and which extrinsically?
Recall that you get a torus by identifying the sides of a rectangle as
in Figure 2.10 of SS (The Shape of Space).
If you identify the sides slightly differently,
as in Figure 4.3, you get a surface called a Klein bottle,
shown in Figure 4.9.
-
Take some strips and join the opposite ends of each strip together as follows:
with no twists;
with one twist (half-turn)-this is called a Möbius strip;
with two twists;
with three twists.
-
Imagine that you are a two-dimensional being who lives in one of these four
surfaces.
To what extent can you tell exactly which one it is?
-
Now cut each of the above along the midline of the original strip.
Describe what you get. Can you explain why?
-
What is the Euler number of a disk? A Möbius strip?
A torus with a circular hole cut from it?
A Klein bottle?
A Klein bottle with a circular hole cut from it?
-
What is the maximum number of points in the plane such that you can draw
non-intersecting segments joining each pair of points?
What about on a sphere? On a torus?
Next: How to knit
Up: Geometry and the Imagination
Previous: Topology
Peter Doyle