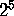 ways, because each intersection can be converted into a crossing
in two ways.
These 32 diagrams will not represent 32 different knots, however.
ways, because each intersection can be converted into a crossing
in two ways.
These 32 diagrams will not represent 32 different knots, however.
A unicursal curve in the plane is a curve that you get when you put down your pencil, and draw until you get back to the starting point. As you draw, your pencil mark can intersect itself, but you're not supposed to have any triple intersections. You could say that you pencil is allowed to pass over an point of the plane at most twice. This property of not having any triple intersections is generic: If you scribble the curve with your eyes closed (and somehow magically manage to make the curve finish off exactly where it began), the curve won't have any triple intersections.
A unicursal curve differs from the curves shown in knot diagrams in that there is no sense of the curve's crossing over or under itself at an intersection. You can convert a unicursal curve into a knot diagram by indicating (probably with the aid of an eraser), which strand crosses over and which strand crosses under at each of the intersections.
A unicursal curve with 5 intersections can be converted into a knot diagram
in 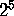 ways, because each intersection can be converted into a crossing
in two ways.
These 32 diagrams will not represent 32 different knots, however.
ways, because each intersection can be converted into a crossing
in two ways.
These 32 diagrams will not represent 32 different knots, however.