 hexascopic;
hexascopic;
 tetrascopic;
tetrascopic;
 triscopic;
triscopic;
 discopic;
discopic;
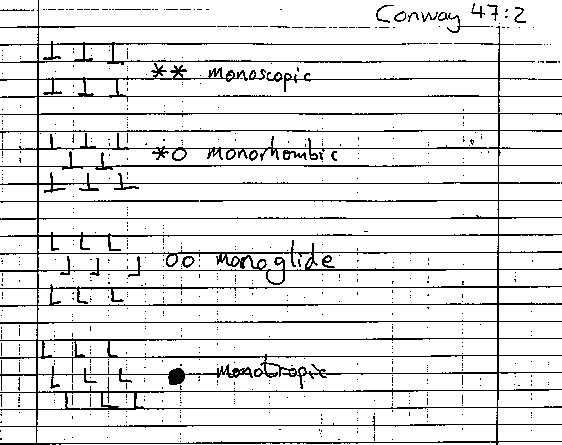
 monoscopic;
monoscopic;
The number 17 is just right for the number of types of symmetry patterns in the Euclidean plane: neither too large nor too small. It's large enough to make learning to recognize them a challenge, but not so large that this is an impossible task. It is by no means necessary to learn to distinguish the 17 types of patterns quickly, but if you learn to do it, it will give you a real feeling of accomplishment, and it is a great way to amaze and overawe your friends, at least if they're a bunch of nerds and geeks.
In this section, we will give some hints about how to learn to classify the patterns. However, we want to emphasize that this is a tricky business, and the only way to learn it is by hard work. As usual, when you analyze a pattern, you should look first for the mirror strings. The information in this section is meant as a way that you can learn to become more familiar with the 17 types of patterns, in a way that will help you to distinguish between them more quickly, and perhaps in some cases to be able to classify some of the more complicated patterns without seeing clearly and precisely what the quotient is. This kind of superficial knowledge is no substitute for a real visceral understanding of what the quotient orbifold is, and in every case you should go on and try to understand why the pattern is what you say it is while your friends are busy admiring your cleverness.
This information presented in this section has been gleaned from a cryptic manuscript discovered among the personal papers of John Conway after his death. For each of the 17 types of patterns, the manuscript shows a small piece of the pattern, the notation for the quotient orbifold, and Conway's idiosyncratic pidgin-Greek name for the corresponding pattern. These names are far from standard, and while they are unlikely ever to enter common use, we have found from our own experience that they are not wholly useless as a method for recognizing the patterns.
We will begin by discussing Conway's names for the orbifolds. A reproduction of Conway's manuscript appears at the end of the section. You should refer to the reproduction as you try to understand the basis for the names.
Each of Conway's 17 names consists of two parts, a prefix and a descriptor.
The prefix tells the number of directions from which you can view the pattern without noticing any difference. The possibilities for the prefix are: hexa-; tetra-; tri-; di-; mono-.
For example, if you are looking at a standard brick wall, it will look essentially the same whether you stand on your feet or on your head. This will be true even if the courses of bricks in the wall do not run parallel to the ground, as they invariably do. Thus you can recognize right away that the brick-wall pattern is di-something-or-other In fact, it is dirhombic.
Another way to think about this is that if you could manage to turn the brick wall upside down, you wouldn't notice the difference. Again, this would be true even if you kept your head tilted to one side. More to the point, try looking at a dirhombic pattern drawn on a sheet of paper. Place the paper at an arbitrary angle, note what the pattern looks like in the large, and rotate the pattern around until it looks in the large like it did to begin with. When this happens, you will have turned the paper through half a rev. No matter how the pattern is tilted originally, there is always one and only one other direction from which it appear the same in the large.
This `in the large' business means that you are not supposed to notice if, after twisting the paper around, the pattern appears to have been shifted by a translation. You don't have to go grubbing around looking for some pesky little point about which to rotate the pattern. Just take the wide, relaxed view.
The descriptor represents an attempt on Conway's part to unite patterns that seem more like each other than they do like the other patterns. The possibilities for the descriptor are: scopic; tropic; gyro; glide; rhombic.
The scopic patterns are those that emerge from kaleidoscopes:
 hexascopic;
hexascopic;
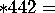 tetrascopic;
tetrascopic;
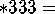 triscopic;
triscopic;
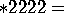 discopic;
discopic;
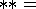 monoscopic;
monoscopic;
Their  -less counterparts
are the tropic patterns (from the Greek for `turn'):
-less counterparts
are the tropic patterns (from the Greek for `turn'):
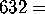 hexatropic;
hexatropic;
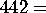 tetratropic;
tetratropic;
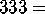 tritropic;
tritropic;
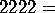 ditropic;
ditropic;
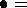 monotropic.
monotropic.
With the scopic patterns, it's all done with mirrors,
while with the tropic patterns,
it's all done with gyration points.
The two exceptions are:
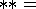 monoscopic;
monoscopic;
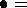 monotropic.
There is evidence that Conway did not consider these
to be exceptions, on the grounds that
`with the scopics it's all done with mirrors and translations,
while with the tropics,
it's all done with turnings and translations'.
monotropic.
There is evidence that Conway did not consider these
to be exceptions, on the grounds that
`with the scopics it's all done with mirrors and translations,
while with the tropics,
it's all done with turnings and translations'.
The gyro patterns contain both mirrors and gyration points:
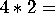 tetragyro;
tetragyro;
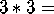 trigyro;
trigyro;
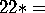 digyro.
digyro.
Since both tropic and gyro patterns involve gyration points,
there is a real possibility of confusing the names.
Strangely, it is the tropic patterns that are the more closely
connected to gyration points.
In practice, it seems to be easy enough to draw this distinction
correctly,
probably because the tropics correspond closely to the scopics,
and `tropic' rhymes with `scopic'.
Conway's view appears to have been that a gyration point,
which is a point of rotational symmetry that does NOT
lie on a mirror,
becomes ever so much more of a gyration point when there are mirrors
around that it might have been tempted to lie on,
and that therefore patterns that contain both gyration points and
mirrors are more gyro than patterns with gyration points but no
mirrors.
The glide patterns involve glide-reflections:
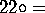 diglide;
diglide;
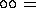 monoglide.
monoglide.
The glide patterns are the hardest to recognize. The quotient orbifold of the diglide pattern is a projective plane with two cone points; the quotient of the monoglide patterns is a Klein bottle. When you run up against one of these patterns, you just have to sweat it out. One trick is that when you meet something that has glide-reflections but not much else, then you decide that it must be either a diglide or a monoglide, and you can distinguish between them by deciding whether it's a di- or a mono- pattern, which is a distinction that is relatively easy to make. Another clue to help distinguish these two cases is that a diglide pattern has glides in two different directions, while a monoglide has glides in only one direction. Yet another clue is that in a monoglide you can often spot two disjoint Möbius strips within the quotient orbifold, corresponding to the fact that the quotient orbifold for a monoglide pattern is a Klein bottle, which can be pieced together from two Möbius strips. These two disjoint Möbius strips arise from the action of glide-reflections along parallel but inequivalent axes.
The rhombic patterns often give a feeling of rhombosity:
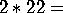 dirhombic;
dirhombic;
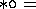 monorhombic.
monorhombic.
An ordinary brick wall is dirhombic; it can be made monorhombic by breaking the gyrational symmetry. The quotient of a monorhombic pattern is a Möbius strip. Like the two glide quotients, it is non-orientable, but it is much easier to identify because of the presence of the mirrors.
As you will see, Conway's manuscript shows only a small portion of each of the patterns. A very worthwhile way of becoming acquainted with the patterns is to draw larger portions of the patterns, and then go through and analyze each one, to see why it has the stated notation and name. You may wish to make flashcards to practice with. When you use these flashcards, you should make sure that you can not only remember the correct notation and name, but also that you can analyze the pattern quickly, locating the distinguishing features. This is important because the patterns you will see in the real world won't be precisely these ones.
Another hint is to keep your eyes open for symmetrical patterns in the world around you. When you see a pattern, copy it onto a flashcard, even if you cannot analyze it immediately. When you have determined the correct analysis, write it on the back and add it to your deck.
What follows is an exact reproduction of Conway's manuscript. In addition to the 17 types of repeating patterns, Conway's manuscript also gives tables of the 7 types of frieze patterns, and of the 14 types of symmetrical patterns on the sphere. These parts of the manuscript appear to be mainly gibberish. We reproduce these tables here in the hope that they may someday come to the attention of a scholar who will be able to make sense of them.