Clocks and curvature
Next: Photographic polyhedron
Up: Geometry and the Imagination
Previous: The celestial image
The total curvature of any surface topologically equivalent to the sphere
is 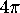 .
This can be seen very simply
from the definition of the curvature of a region
in terms of the angle of rotation when the surface
is rolled around on the plane;
the only problem is the perennial one of
keeping proper track of multiples of
.
This can be seen very simply
from the definition of the curvature of a region
in terms of the angle of rotation when the surface
is rolled around on the plane;
the only problem is the perennial one of
keeping proper track of multiples of 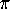 when measuring the angle of
rotation.
Since are trying to show that the total curvature is a specific multiple of
when measuring the angle of
rotation.
Since are trying to show that the total curvature is a specific multiple of
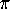 ,
this problem is crucial.
So to begin with let's think carefully about
how to reckon these angles correctly
,
this problem is crucial.
So to begin with let's think carefully about
how to reckon these angles correctly
Suppose we have a number of clocks on the wall.
These clocks are good mathematician's clocks, with a 0 up at the top where
the 12 usually is.
(If you think about it,
0 o'clock makes a lot more sense than 12 o'clock:
With the 12 o'clock system,
a half hour into the new millennium on 1 Jan 2001,
the time will be 12:30 AM, the 12 being some kind of hold-over from the
departed millennium.)
Let the clocks be labelled 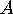 ,
, 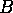 ,
, 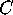 , ....
To start off, we set all the clocks to 0 o'clock.
(little hand on the 0; big hand on the 0),
Now we set clock
, ....
To start off, we set all the clocks to 0 o'clock.
(little hand on the 0; big hand on the 0),
Now we set clock 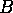 ahead half an hour
so that it now the time it tells is 0:30
(little hand on the 0 (as they say); big hand on the 6).
What angle does its big hand make with that of clock
ahead half an hour
so that it now the time it tells is 0:30
(little hand on the 0 (as they say); big hand on the 6).
What angle does its big hand make with that of clock 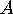 ?
Or rather, through what angle has its big hand moved relative to that
of clock
?
Or rather, through what angle has its big hand moved relative to that
of clock 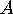 ?
The angle is
?
The angle is 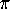 .
If instead of degrees or radians, we measure our angles in revs
(short for revolutions),
then the angle is
.
If instead of degrees or radians, we measure our angles in revs
(short for revolutions),
then the angle is 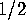 rev.
We could also say that the angle is
rev.
We could also say that the angle is 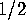 hour:
as far as the big hand of a clock is concerned,
an hour is the same as a rev.
hour:
as far as the big hand of a clock is concerned,
an hour is the same as a rev.
Now take clock 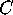 and set it to 1:00.
Relative to the big hand of clock
and set it to 1:00.
Relative to the big hand of clock 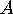 , the big hand of
, the big hand of 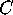 has moved
through an angle of
has moved
through an angle of 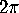 , or 1 rev, or 1 hour.
Relative to the big hand of
, or 1 rev, or 1 hour.
Relative to the big hand of 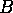 , the big hand of
, the big hand of 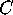 has moved through
an angle of
has moved through
an angle of 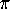 , or
, or 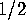 rev.
Relative to the big hand of
rev.
Relative to the big hand of 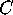 , the big hand of
, the big hand of 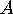 has moved through
an angle of
has moved through
an angle of 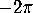 , or
, or 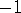 rev,
and the big hand of
rev,
and the big hand of 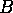 has moved
has moved 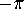 , or
, or 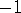 rev.
rev.
Now let's describe how to find the curvature inside a disk-like region 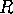 on a surface
on a surface 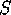 , i.e. a region topologically equivalent to a disk.
What we do is cut a small circular band running around the boundary of the
region, cut the band open to form a thin strip, lay the thin strip
flat on the plane,
and measure the angle between the lines at the two end of the strip.
In order to keep the
, i.e. a region topologically equivalent to a disk.
What we do is cut a small circular band running around the boundary of the
region, cut the band open to form a thin strip, lay the thin strip
flat on the plane,
and measure the angle between the lines at the two end of the strip.
In order to keep the  's straight,
let us go through this process very slowly and carefully.
's straight,
let us go through this process very slowly and carefully.
To begin with, let's designate the two ends of the strip
as the left end and the right end in such a way that
traversing the strip from the left end to the right end
corresponds to circling clockwise around the region.
We begin by fixing the left-hand end of the strip to the wall so that
the straight edge of the cut at the left end of the strip-the cut that
we made to convert the band into a strip-runs
straight up and down, parallel to the big hand of clock 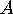 ,
and so that the strip runs off toward the right.
Now we move from left to right along the strip,
i.e. clockwise around the boundary of the region,
fixing the strip so that
it lies as flat as possible, until we come to the right end of the strip.
Then we look at the cut bounding the right-hand end of the strip,
and see how far it has turned relative to the left-hand end of the strip.
Since we were so careful in laying out the left-hand end of the strip,
our task in reckoning the angle of the right-hand end of the strip
amounts to deciding what time you get if you think of the right-hand end
of the strip as the big hand of a clock.
The curvature inside the region will correspond to the amount by which the time
told by the right-hand end of the strip falls short of 1:00.
,
and so that the strip runs off toward the right.
Now we move from left to right along the strip,
i.e. clockwise around the boundary of the region,
fixing the strip so that
it lies as flat as possible, until we come to the right end of the strip.
Then we look at the cut bounding the right-hand end of the strip,
and see how far it has turned relative to the left-hand end of the strip.
Since we were so careful in laying out the left-hand end of the strip,
our task in reckoning the angle of the right-hand end of the strip
amounts to deciding what time you get if you think of the right-hand end
of the strip as the big hand of a clock.
The curvature inside the region will correspond to the amount by which the time
told by the right-hand end of the strip falls short of 1:00.
For instance, say the region 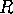 is a tiny disk in the Euclidean plane.
When we cut a strip from its boundary and lay it out as described above,
the time told by its right hand end will be precisely 1:00, so the curvature
of
is a tiny disk in the Euclidean plane.
When we cut a strip from its boundary and lay it out as described above,
the time told by its right hand end will be precisely 1:00, so the curvature
of 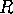 will be exactly 0.
If
will be exactly 0.
If 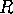 is a tiny disk on the sphere, then when the strip is laid out the time
told will be just shy of 1:00, say 0:59, and the curvature of the region
will be
is a tiny disk on the sphere, then when the strip is laid out the time
told will be just shy of 1:00, say 0:59, and the curvature of the region
will be 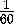 rev, or
rev, or 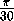 .
.
When the region 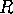 is the lower hemisphere of a round sphere,
the strip you get will be laid out in a straight line,
and the time told by the right-hand end will be 0:00,
so the total curvature will be 1 rev, i.e.
is the lower hemisphere of a round sphere,
the strip you get will be laid out in a straight line,
and the time told by the right-hand end will be 0:00,
so the total curvature will be 1 rev, i.e. 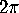 .
The total curvature of the upper hemisphere is
.
The total curvature of the upper hemisphere is 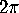 as well,
so that the total curvature of the sphere is
as well,
so that the total curvature of the sphere is 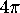 .
.
Another way to see that the total curvature of the sphere is 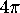 is to take as the region
is to take as the region 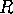 the outside of a small circle on the
sphere.
When we lay out a strip following the prescription above, being sure to
traverse the boundary of the region
the outside of a small circle on the
sphere.
When we lay out a strip following the prescription above, being sure to
traverse the boundary of the region 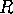 in the clockwise sense as viewed
from the point of view of the region
in the clockwise sense as viewed
from the point of view of the region 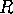 , we see that the time told by the
right hand end of the strip is very nearly
, we see that the time told by the
right hand end of the strip is very nearly 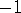 o'clock!
The precise time will be just shy of this,
say
o'clock!
The precise time will be just shy of this,
say 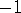 :59,
and the total curvature of the region will then be
:59,
and the total curvature of the region will then be 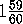 revs.
Taking the limit,
the total curvature of the sphere is 2 revs, or
revs.
Taking the limit,
the total curvature of the sphere is 2 revs, or 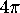 .
.
But this last argument will work equally well on any surface topologically
equivalent to a sphere, so any such surface has total curvature 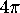 .
.
This proof that the total curvature of a topological sphere is 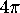 gives the definite feeling of being some sort of trick.
How can we get away without doing any work at all?
And why doesn't the argument work equally well on a torus, which as we know should have total curvature 0? What gives?
gives the definite feeling of being some sort of trick.
How can we get away without doing any work at all?
And why doesn't the argument work equally well on a torus, which as we know should have total curvature 0? What gives?
What gives is the lemma that states that if you take a disklike region 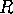 and divide it into two disklike subregions
and divide it into two disklike subregions 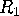 and
and 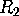 , then the
curvature inside
, then the
curvature inside 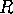 when measured by laying out its boundary is the sum
of the curvatures inside
when measured by laying out its boundary is the sum
of the curvatures inside 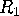 and
and 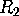 measured in this way.
This lemma might seem like a tautology.
Why should there be anything to prove here?
How could it fail to be the case that the curvature inside the whole is
the sum of the curvatures inside the parts?
The answer is,
it could fail to be the case by virtue of our having given a faulty definition.
When we define the curvature inside a region, we have to make sure that the
quantity we're defining has the additivity property, or the definition is no
good.
Simply calling some quantity the curvature inside the region will not make
it have this additivity property.
For instance, what if we had defined the curvature inside a region to be
measured in this way.
This lemma might seem like a tautology.
Why should there be anything to prove here?
How could it fail to be the case that the curvature inside the whole is
the sum of the curvatures inside the parts?
The answer is,
it could fail to be the case by virtue of our having given a faulty definition.
When we define the curvature inside a region, we have to make sure that the
quantity we're defining has the additivity property, or the definition is no
good.
Simply calling some quantity the curvature inside the region will not make
it have this additivity property.
For instance, what if we had defined the curvature inside a region to be
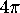 , no matter what the region?
More to the point, what if in the definition of the curvature inside
a region we had forgotten the proviso that the region
, no matter what the region?
More to the point, what if in the definition of the curvature inside
a region we had forgotten the proviso that the region 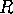 be disklike?
Think about it.
be disklike?
Think about it.
Next: Photographic polyhedron
Up: Geometry and the Imagination
Previous: The celestial image
Peter Doyle
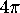 .
This can be seen very simply
from the definition of the curvature of a region
in terms of the angle of rotation when the surface
is rolled around on the plane;
the only problem is the perennial one of
keeping proper track of multiples of
.
This can be seen very simply
from the definition of the curvature of a region
in terms of the angle of rotation when the surface
is rolled around on the plane;
the only problem is the perennial one of
keeping proper track of multiples of 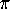 when measuring the angle of
rotation.
Since are trying to show that the total curvature is a specific multiple of
when measuring the angle of
rotation.
Since are trying to show that the total curvature is a specific multiple of
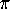 ,
this problem is crucial.
So to begin with let's think carefully about
how to reckon these angles correctly
,
this problem is crucial.
So to begin with let's think carefully about
how to reckon these angles correctly
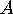 ,
, 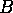 ,
, 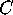 , ....
To start off, we set all the clocks to 0 o'clock.
(little hand on the 0; big hand on the 0),
Now we set clock
, ....
To start off, we set all the clocks to 0 o'clock.
(little hand on the 0; big hand on the 0),
Now we set clock 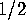 rev.
We could also say that the angle is
rev.
We could also say that the angle is 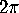 , or 1 rev, or 1 hour.
Relative to the big hand of
, or 1 rev, or 1 hour.
Relative to the big hand of 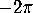 , or
, or 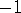 rev,
and the big hand of
rev,
and the big hand of 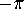 , or
, or 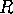 on a surface
on a surface 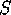 , i.e. a region topologically equivalent to a disk.
What we do is cut a small circular band running around the boundary of the
region, cut the band open to form a thin strip, lay the thin strip
flat on the plane,
and measure the angle between the lines at the two end of the strip.
In order to keep the
, i.e. a region topologically equivalent to a disk.
What we do is cut a small circular band running around the boundary of the
region, cut the band open to form a thin strip, lay the thin strip
flat on the plane,
and measure the angle between the lines at the two end of the strip.
In order to keep the 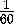 rev, or
rev, or 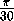 .
.
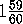 revs.
Taking the limit,
the total curvature of the sphere is 2 revs, or
revs.
Taking the limit,
the total curvature of the sphere is 2 revs, or 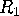 and
and 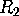 , then the
curvature inside
, then the
curvature inside