 ?
Well, no. What values can the sum of the angles take on?
?
Well, no. What values can the sum of the angles take on?
We want to explore some aspects of geometry on the surface of the sphere. This is an interesting subject in itself, and it will come in handy later on when we discuss Descartes's angle-defect formula.
Great circles on the sphere are the analogs of straight lines in the plane. Such curves are often called geodesics. A spherical triangle is a region of the sphere bounded by three arcs of geodesics.
 ?
Well, no. What values can the sum of the angles take on?
?
Well, no. What values can the sum of the angles take on?
The area of a spherical triangle is the amount by which the sum of its
angles exceeds the sum of the angles (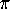 ) of a Euclidean triangle.
In fact, for any spherical polygon, the sum of its angles minus the
sum of the angles of a Euclidean polygon with the same number of sides
is equal to its area.
) of a Euclidean triangle.
In fact, for any spherical polygon, the sum of its angles minus the
sum of the angles of a Euclidean polygon with the same number of sides
is equal to its area.
A proof of the area formula can be found in Chapter 9 of Weeks, The Shape of Space.