Previous: Calculation of Geodesics
Up: The Mathematics of Orbifold Pinball
Previous: Calculation of Geodesics
Up: The Mathematics of Orbifold Pinball
Here are the steps of the algorithm in the case of the orbifold.
Step#1. The Euler number of is
, so this orbifold is really hyperbolic.
Step#2. Make branch cuts connecting the -point to all
-points. Unbend the
sphere and you get a hyperbolic hexagon with angles
,
,
and three angles whose sum is
, i.e three zero-angles.
Angles
degenerate to the hyperbolic lines (which are arcs orthogonal to the unit circle). So we get a hyperbolic triangle with all angles
. In the hyperbolic geometry the angle
can be located only at
(on the boundary of the Poincare circle).
We choose the configuration of the triangle to be as symmetric as we can. For this
the cone points of order
have to be located in the middle of each side (they identify two halves of each side by a
rotation). We also make the triangle equilateral. We may suppose one of the vertices is 1 (the others then will be
and
). Note that rotations identify all three vertices to one.
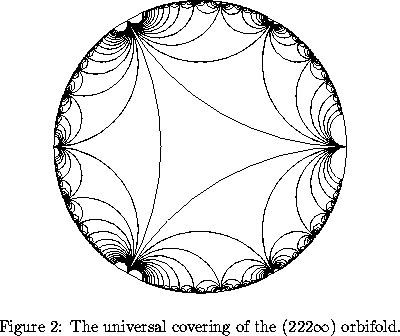
Step#3. Now let's see how this orbifold looks. The choice of the fundamental domain completely determines how the singular points are located w.r.t. each other but we still can rotate and translate them on the sphere. So for convenience let us put the cone point of order at the north pole, i.e. to infinity. Now the symmetry really helps us. All cone points of order
are logically equivalent and in the universal covering we made them be absolutely symmetric. This tells us that they should be absolutely symmetric on the sphere. Switching for convenience to the plane with infinity, they have to be at the vertices of an equilateral triangle. Rescaling and rotation place one vertex at 1. The branch cuts will become rays connecting the vertices of this triangle to infinity. And again the absolute symmetry tells us that these rays will come to infinity with angles
,
,
. So step 3 is stated now as follows:
Find a conformal mapping of the outside of three symmetric rays onto the curvilinear triangle with angles 0. The ends of the rays should go to the middles of the sides of the triangle and complex infinity should go to the vertices of the triangle.
I solved this problem in several steps. The most crucial step was in using the inverse of the elliptic modular function which maps the upper half plane onto the modular triangle with angles . Here it is the cute formula:
where
Unfortunately this happened to be a very slow way to calculate the function (and its inverse) on the computer. I had to precalculate a huge table of values of this function (this took three days of computer computations) and then to use Lagrange cubic interpolation to find the value of the function at specific points.
Step#4. In the same way I approximated the derivative of the function, which basically completes this step.
Step#5. When I hit the boundary I use hyperbolic rotations by degrees around the middle of the corresponding side.
Step#6. This step is the inverse of step 3.