Previous: The Mathematics of Orbifold Pinball
Up: The Mathematics of Orbifold Pinball
Next: Conway's Notation and the Euler Number
Previous: The Mathematics of Orbifold Pinball
Up: The Mathematics of Orbifold Pinball
Next: Conway's Notation and the Euler Number
An orbifold is a Hausdorff space which is locally
homeomorphic at each point
to
, where
is some finite group, perhaps different for different
.
The set of
s.t.
(in other words, points
no neighborhood of which is homeomorphic to
) is called the
singular locus of the orbifold
.
An orbifold is called good if it has a covering which is a manifold.
The following amazing theorem is true for 2-orbifolds:
The singular locus of a 2-orbifold has only three possible types of local model:
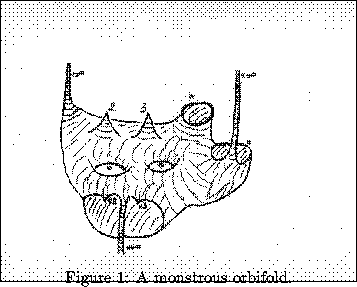
Here is an example which shows some of the features a 2-orbifold may have: