Hippias' Quadratrix

Around 420 B.C., Hippias of Elis discovered a quadratrix curve (also known as a trisectrix). Hippias' quadratrix was the first curve in recorded history that was not part of a line or a circle [2, p.40]. The definition of the quadratrix is the following.

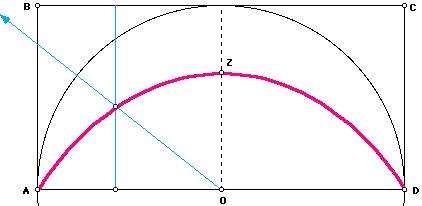A segment AB translates uniformly from AB to CD at the same time ray OA rotates about point O uniformly clockwise until it reaches OD. The curve traced out by the intersection of the segment and the ray is the quadratrix. [2, p.41]

You may experience this curve in Geometer's Sketchpad by clicking on Hippias' quadratrix sketch. Note that this curve was not "constructed" in the classical Greek sense of the word. It is theoretically possible to construct a countable set of points on the curve using only a compass and a straight edge. However, this is not good enough to be a true construction. Although points on the quadratrix may be found as close to each other as desired, there are alway missing points. To truely construct a set of points on the quadratrix, click on the true construction of points on Hippias' quadratrix. Despite the construction problem, the quadratrix can be made to any desired precision.

So what does this curve have to do with ? It was proven by Dinostrus around 335 B.C. that the quadratrix could be used to square the circle, i.e. construct a square with the same area as a circle. By starting with the unit circle, the construced square would have sides of length thus finding the value of . Actually, the quadratrix was rectified by Dinostrus, but a rectangle can easily be squared. The rectangle with the same area as the unit circle centered at O with radius OA has sides of length OA and (AD^2)/(2*OZ), where Z is the point on the quadrartix and the perpendicular bisector of AD. In fact AD/OZ = . (The proof is not given here, but may be found in [2, p.41].)

The "stumbling block" of squaring the circle is that point Z on the quadratrix can not be constructed! In fact, Hippias' definition of the quadratrix fails at point Z. Try tracing out Hippias' quadratrix again in Geometer's Sketchpad. Notice what happens as you near creating point Z. The intersection of the segment and the ray is the entire segment rather than just a point. Using the idea of a limit, point Z can be found, but not constructed. (In fact, point Z relies on the fact that as x approaches 0, sin(x)/x approaches 1.)

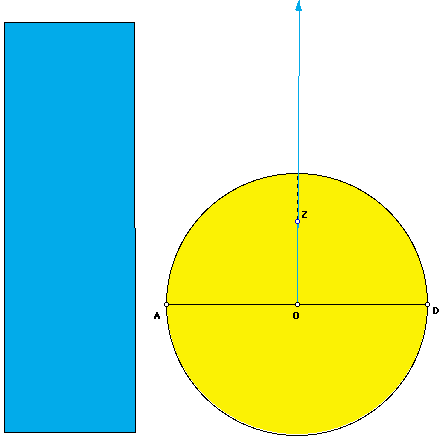
Nonetheless, we are able to approximate the rectification of the quadratrix with Geometer's Sketchpad. The circle has area r^2. The rectangle is given with sides of length OA and (AD^2)/(2*"drag"L). As you move point "drag" to O, point L approaches Z, and the area of the rectangle approaches the area of the circle. By dividing the area of the rectangle by r^2, we get .

Rectified Circle Using Hippias' Quadratrix

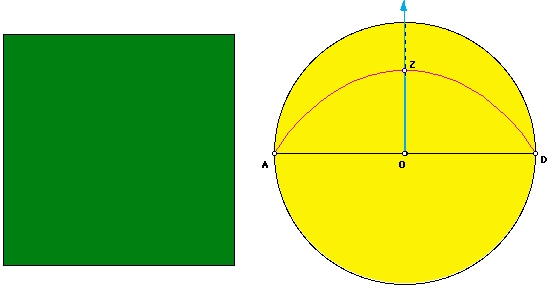
Since a rectangle can easily be squared, we now can use Geometer's Sketchpad to show Hippias' quadratrix squared.

Squared Circle Using Hippias' Quadratrix

Return to Historical Overview of Pi

Go to A Slice of Pi Home Page