Pi & Fibonacci Numbers

Recall that the Fibonacci sequence is defined by F(1) = 1, F(2) = 1, F(3) = 2, F(n) + F(n+1) = F(n+2). The following relation involving the Fibonacci numbers was proven by Ko Hayashi [3].

(*)

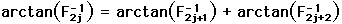
The connection to is that arctan(1) = /4. Thus can be expressed in terms of Fibonacci numbers

The first three cases have been demonstrated geometrically using the Geometer's Sketchpad. (These are not really interactive sketches.)

• arctan(1) = arctan (1/2) + arctan(1/3)

• green angle = arctan(1) (look at the 1x1 square)
• red angle = arctan(1/2) (look at the tilted 1x2 rectangle)
• blue angle = arctan(1/3) (look at the 1x3 rectangle)

One can easily see that green angle = red angle + blue angle.
Thus we have ¼/4 = arctan(1) = arctan (1/2) + arctan(1/3).

• arctan(1/3) = arctan(1/5) + arctan(1/8)

As it is difficult to see the angles involved here, the following picture zooms in on the important angles.

• blue angle = arctan(1/3) as before (look at a 1x3 rectangle)
• yellow angle = arctan(1/5) (look at the tilted 1x5 rectangle)
• pink angle = arctan(1/8) (look at the 1x8 rectangle)

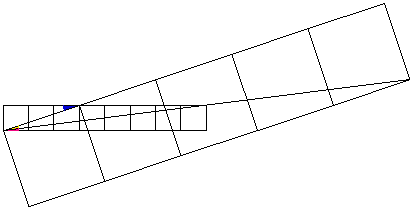
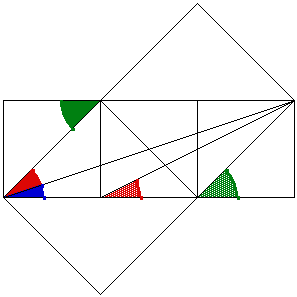
Again, it is easy see that blue angle = yellow angle + pink angle.
Thus we have arctan(1/3) = arctan (1/5) + arctan(1/8).
Combining this with the previous result yields ¼/4 = arctan(1) = arctan (1/2) + arctan (1/5) + arctan(1/8).

• arctan(1/8) = arctan(1/13) + arctan(1/21)

It is extremely difficult to see the angles involved here, so again the following picture zooms in on the important angles.

• pink angle = arctan(1/8) as before (look at a 1x8 rectangle)
• cyan angle = arctan(1/13) (look at the tilted 1x13 rectangle)
• black angle = arctan(1/8) (look at the difficult to see 1x21 rectangle)

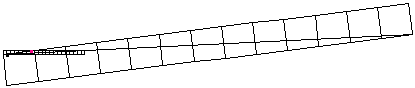
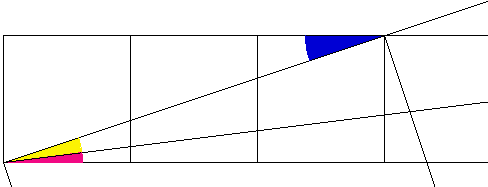
Again, it is easy see that pink angle = cyan angle + black angle.
Thus we have arctan(1/8) = arctan (1/13) + arctan(1/21).
Combining this with previous results yields ¼/4 = arctan(1) = arctan (1/2) + arctan (1/5) + arctan (1/13) + arct an(1/21).

, for any natural number n.

Each sum starting with n =1, is an exact representation of . One can look at four times the summation to be a partial sum with

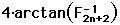
as the error term for . The sequence of these partial sums converges to also. I.e.,

.

Using the formula for the tangent of the sum of two angles, these relationships can be easily verified.

Return to Historical Overview of Pi

Go to A Slice of Pi Home Page